해당 포스팅의 모든 자료는 CS224W 강의 및 관련 자료를 바탕으로 정리하였습니다.
0. 들어가기에 앞서
저번 포스팅에서는 graph의 feature들을 어떻게 design 할 것인지에 대해 feature-based methods를 nodel level, link level 에서 알아보았다. 이번 포스팅에서는 graph level에서 어떻게 feature들을 design할 것인지 알아보자.
1. Graph-Level Features
수업의 목표는 전체 graph의 전체 구조를 characterize하는 feature를 잡아내는 방법에 대해 배우는 것이다.
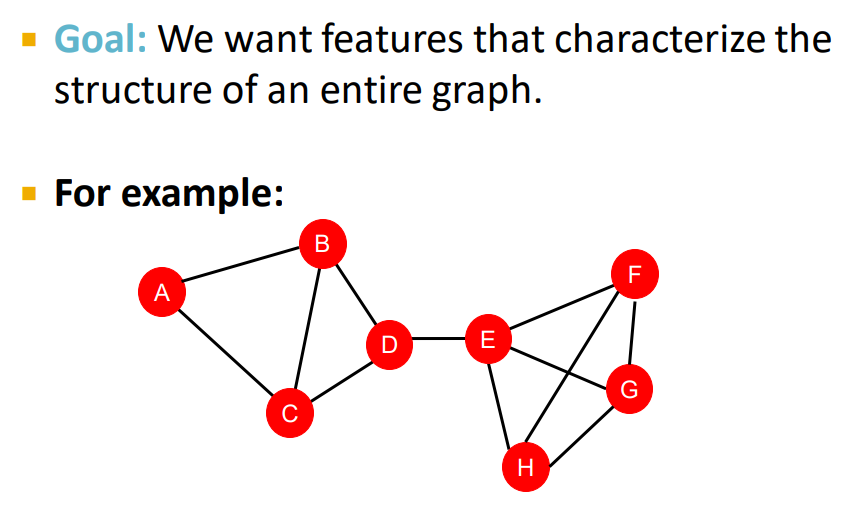
위 예시를 보면 A,B,C,D로 이루어진 부분과 E,F,G,H로 이루어진 부분이 D-E link 하나로 연결되어있다.
이러한 graph의 위와 같은 feature을 어떻게 하면 잘 잡아낼 수 있을까?
이를 잘 잡아내기 위해 Kernel methods라는 것을 사용할 것이다.

Kernel methods는 graph-level prediction 등의 전통적인 머신러닝에서 사용되는 방법이다.
아이디어는 feature vector 대신 특정 kernel K를 만들어내는것이다. 이 kernel K는 핵심적인 정보를 담고있다.
K(G, G')는 실제 value값을 반환하고, 두 그래프 G와 G' 혹은 두개의 서로 다른 data point에 대한 유사도를 계산한다.
Kernel matrix K는 positive semi-definite(준정정행렬)이여야한다. 그리고 Kernel matrix는 feature vector를 생성하는 ϕ(Phi)의 내적 곱으로 이를 나타낼 수 있다. 커널을 정의한 후에는, Kernel SVM과 같은 방법으로 feature를 예측할 수 있다.

강의에서는 유사도를 측정하는 서로 다른 두 Graph Kernels를 배울 것이다.
1. Graphlet Kernel
2. Weisfeiler-Lehman Kernel
random-walk kernel, shortest-path kernel 등의 다양한 kernel이 있지만 해당 강의에서는 다루지 않는다고 한다.
그리고 일반적으로, 이 두 kernel만 알고있어도 graph-level task에서 매우 좋은 성능을 낼 수 있다.
우선 Kernel은 왜 필요한 것일까?
Kernel이 필요한 이유는 Kernel을 활용해 feature vector를 정의할 수 있기 때문이다.
즉 위에서 나왔던 ϕ(G)(=feature vector)를 Kernel을 활용해 찾을 수 있다.
여기서 핵심 아이디어는 바로 이 ϕ(G)를 Bag-of-words 형태의 graph representation이라고 생각하는 것이다.
Bag-of-words는 일반적으로 텍스트(in nlp)에서 어떤 단어가 특정 documents에 몇 번 들어가 있는지(순서 고려 x)를 수치화 한 데이터 표현 방법이다.Bag-of-words 형태를 graph에서 적용한다는 것은 node를 이러한 단어로 생각하면 이해하기 쉽다.
그러나 위의 ϕ 함수 안에있는 graph와 같이 node의 개수가 동일하다면, 다른 graph여도 같은 feature vector로서 표현되는 단점이 있다.
이러한 문제는 Bag of nodes가 아닌 Bag of node degrees를 사용해서 해결할 수 있다.
Bag of node degrees를 사용하면 아래의 그림에서 node의 개수만 같은 서로 다른 두 그래프에 대해 [1,2,1]과 [0,2,2]라는 다른 features vector를 반환한다.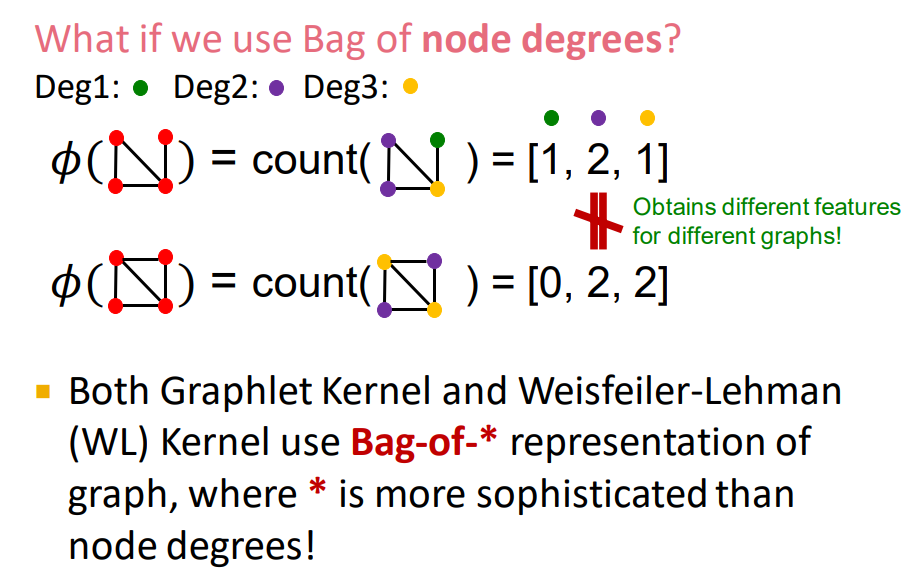
그렇다면 이제 본격적으로 두가지 kerenl 중 첫번째인 Graphlet kernel에 대해 알아보자.
2. Graphlet Kernel
Graphlet kernel은 하나의 graph 안에 있는 서로 다른 graphlets의 수를 세는 방법이다.

이때, 여기서의 graphlet의 정의는 앞에서 배웠던 node-level features에서의 graphlet의 정의와 조금 다르다.
우선 node-level features에서는 graphlets의 nodes가 꼭 연결되어 있을 필요는 없었다.

아래와 같은 graph 예시에서 k = 3이면 가능한 graphlets은 g1,g2,g3,g4이고 결국 feature vector f(g)는 (1,3,6,0)으로 나타낼 수 있다.

이렇게 feature vector인 f(g)를 구했으면 G'에 대한 f(g')도 구한 후 이를 내적하면 K(G,G') 값을 계산할 수 있다.
그러나 문제는 graph G와 G'의 크기가 다를 수 있기 때문에 sum(f(g))로 나눠준 h(g)를 이용해 구한다.(normalize)

그러나 이러한 방식의 한계는 graphlets을 counting하는것이 매우 expensive하다는 것이다.

3. Weisfeiler-Lehman graph kernel
이를 해결하기 위해 나온것이 바로 두번째 kernel이였던 Weisfeiler-Lehman graph kernel이다.
Weisfeiler-Lehman graph kernel의 목표는 효율적인 graph feature descriptor ϕ(G)를 생성하는 것이다.
핵심 아이디어는 neighborhood structure를 반복적으로 이용해 vocabulary(node)를 만들어나가는 것이다.
위에서 언급한 Bag of node degrees 방법을 조금 더 일반화 한 것이라고 볼 수 있다.Bag of node degrees가 one-hop neighborhood information만을 이용한다면,
Weisfeiler-Lehman graph kernel는 multi-hop neighborhood information을 이용한다.
one-hop은 한 다리 건너, multi-hop은 여러 다리 건너 정도로 생각하면 된다.

Weisfeiler-Lehman graph kernel 알고리즘은 Weisfeiler-Lehman graph isomorphism test 혹은 Color refinement라고 불린다.
알고리즘의 순서는 다음과 같다.

graph G가 node set V로 이루어져 있을때,
1. 초기 색 c^(0)(v)를 각 노드 v에 배정한다.
2. 위 초록색 HASH 함수 식을 이용해 c^(k+1)(v)를 만든다.
위 알고리즘을 k step만큼 반복하면, c^(k)(v)는 K-hop neighborhood의 구조를 요약한다.
무슨 말인지 잘 감이 안온다면 아래의 예시를 통해 자세히 살펴보자.
우선 아래와 같은 G1 graph, G2 graph가 있다고 가정해보자.
"1. 초기 색 c^(0)(v)를 각 노드 v에 배정한다." 에 따라 각 노드에 동일한 초기 색(1)을 배정한다.

그 후 이웃 노드의 색(1)들을 concat하여 정보를 모은다.
그 후 "2. 위 초록색 HASH 함수 식을 이용해 c^(k+1)(v)를 만든다." 에 따라 HASH table을 참고하여 해당 정보들을 지정된 색으로 변경한다.

이제 다시 이웃 노드의 색(2~5)들을 concat하여 정보를 모은다.
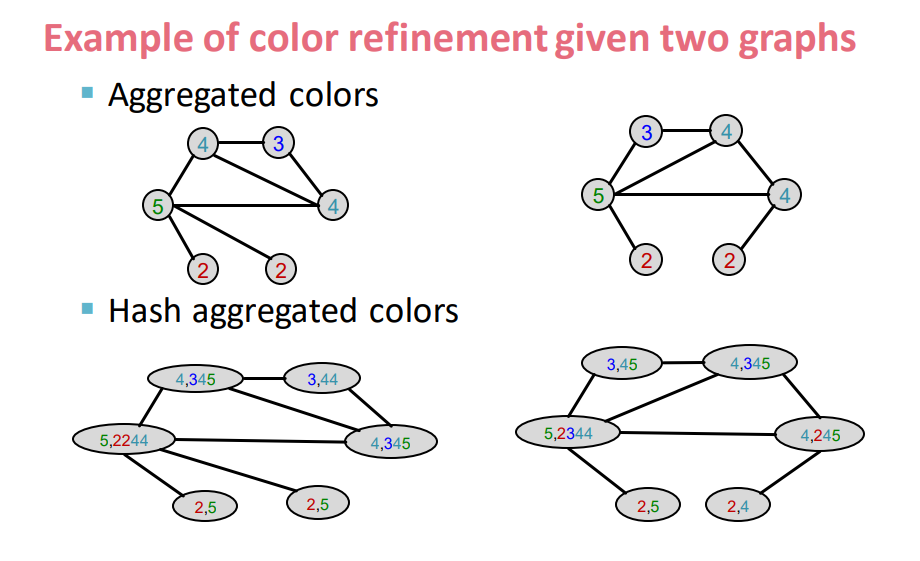
그리고 위에서와 같이 HASH table을 참고하여 색을 변환시켜준다.
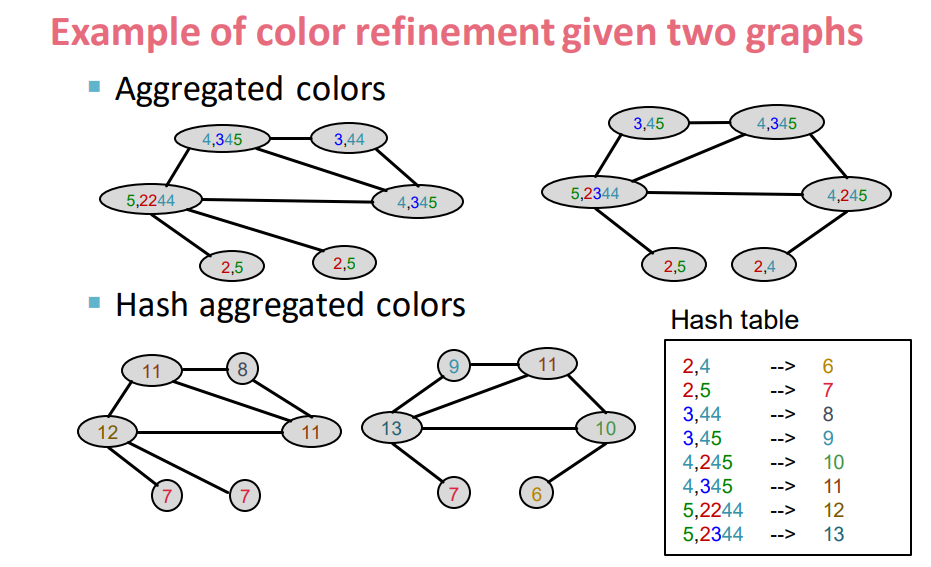
최종적으로 변환된 그래프에는 2-hop에 해당하는 정보가 요약되어 있는 것이다.

이러한 과정을 k 번 거친다고 생각하면 Weisfeiler-Lehman kernel은 HASH table에서 각각의 Colors에 해당하는 값들의 빈도 수를 계산해 리스트(feature descriptors)로 만들고 이것이 graph G에 대한 ϕ(G)가 되는 것이다.
이렇게 구한 ϕ(G1)과 ϕ(G2)를 내적해주면 graph들 사이의 similarity을 구할 수 있다.

Weisfeiler-Lehman kernel 알고리즘은 매우 효율적(복잡도 측면에서)이고 강력한 성능을 지닌다.

정리하자면 graph level에서 feature를 표현하는 방식은 크게 두 가지가 있는데,
1. Graphlet Kernel과 2. Weisfeiler-Lehman Kernel 이다.
1. Graphlet Kernel은 Bag-of-words 형태인 Bag-of-graphlets를 사용하는데, 연산 비용이 많이 든다.
2. Weisfeiler-Lehman Kernel는 Bag-of-colors로 feature를 표현하는데, 연산 비용이 효율적이고 뒤에서 배울 Graph Neural Networks(GNN)과 밀접한 관련이 있다.

댓글