- Reference
Naver d2 이활석님의 '오토인코더의 모든것'
Kaist Edward Choi 교수님의 Programming for AI(AI 504, Fall2020)
Naver d2 이활석님의 '오토인코더의 모든것'과 Kaist Edward Choi 교수님의 AI 504 수업을 토대로 공부한 후 정리하였습니다.
0. 글 쓰기에 앞서
지난번 포스팅에서는 오토인코더의 개념과 특징, 그 중에서도 가장 중요한 특징인 dimensionality reduction(차원축소)에 대해 정리했었다. 또한 차원의 저주를 피하기 위해 Manifold의 관점에서 오토인코더가 어떻게 차원축소를 하는지도 정리했었는데, 이번 포스팅에서는 오토인코더 말고도 Dimensionality Reduction, Density Estimation을 하는 다양한 방법들에 대해 알아보자. 또한 그런 방법들에는 어떠한 문제점이 있어서 오토인코더가 등장했는지도 알아보자.
(지난번 포스팅 -> 오토인코더(Autoencoder)가 뭐에요? - 1.Dimensionality reduction and Maninfold Learning)
오토인코더(Autoencoder)가 뭐에요? - 1.Dimensionality reduction and Maninfold Learning
- Reference Naver d2 이활석님의 '오토인코더의 모든것' Kaist Edward Choi 교수님의 Programming for AI(AI 504, Fall2020) Naver d2 이활석님의 '오토인코더의 모든것'과 Kaist Edward Choi 교수님의 AI 504 수..
hyunsooworld.tistory.com
1. Dimensionality Reduction method

차원 축소를 하는 방법에는 오토인코더 말고도 여러가지가 있다.
크게 Linear한 방법과 Non-Linear한 방법으로 나눌 수 있는데
Linear한 방법에는 PCA, LDA 등이 있고, Non-Linear한 방법에는 AutoEncoder, t-SNE, LLE 등이 있다.
이번 포스팅에서는 PCA, LDA, AE, t-SNE, LLE 에 대해 알아 볼 것이다.
1-1. Linear method(PCA, LDA)
주성분 분석(Principal component analysis)은 고차원의 데이터를 저차원의 데이터로 환원시키는 기법을 말한다. 이 때 서로 연관 가능성이 있는 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간(주성분)의 표본으로 변환하기 위해 직교 변환을 사용한다. (위키백과)
쉽게 말하면 PCA란 데이터를 샘플 공간에 뿌렸을때 분산을 최대화하는 축을 찾는 것이다.

왜 분산을 최대화 하는 축을 찾는 것일까?
그 이유는 바로 분산을 최대로 하는 축이 정보의 손실이 가장 적기 때문이다.
분산이 크면 데이터들의 차이가 크다는 것이고, 데이터간의 차이를 설명할 피처들을 잘 추출하기 때문에 더 좋은 모델을 만들 수 있다.

하지만, PCA는 linear한 방식이기 때문에 manifold가 위와 같이 꼬여있는(?) 경우 잘 구분하지 못한다(Entangled manifold).
PCA는 축소하고자 하는 데이터 간의 공분산행렬을 구하고 고유벡터를 추출해 그 값을 구한다.
🙄 PCA vs AutoEncoders

- PCA와 AutoEncoder 둘 다 reconstruction error를 최소화하는 것이 목적이다.
reconstruction error(재구성 오차) : 원본 데이터와 복원한 데이터간의 평균 제곱 거리
- 그러나 PCA는 Linear transformation(선형변환)이고 Autoencoder는 Non-Linear transformation(비선형변환)이다.
LDA(Linear Discriminant Analysis)는 PCA와 유사하나 조금 더 "분류"에 최적화 되어있는 차원축소 기법이다.

LDA는 투영 후 두 집단 간 분산은 최대한 크게, 집단 내부의 분산은 최대한 작게 가져가는 방식을 택한다.
다시 말해 LDA는 특정 데이터의 클래스를 분리하고자 할때 [(클래스 간 분산)/(클래스 내부 분산)]을 최대화하는 방식으로 차원을 축소한다.
1-2. Non-Linear method(Isomap, LLE)

Isomap과 LLE 두 방법 모두 가까운 이웃을 먼저 구하는 방식으로 알고리즘이 전개된다.
가까운 이웃을 구하는 이유는 굉장히 근접한 이웃의 경우 manifold 상에서도 가까울 것이다 라는 가정이 전제 되어 있기 때문이다.
2. Density Estimation
Density Estimation을 하는 방법으로는 대표적으로 Parzen Windows가 있다.
2-1. Parzen Windows
Parzen Windows는 커널 밀도 추정의 대표적인 방법이다.
커널 밀도 추정(Kernel Density Estimation)이란 무엇일까?
커널밀도추정(KDE)는 커널 함수와 데이터를 이용해 확률 밀도 함수 즉 pdf를 추정하는 것이다.
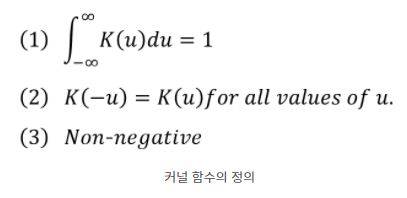
커널밀도추정은 그렇다면 왜 하는 것일까?
일반적으로 통계학에서 밀도(density)는 확률밀도함수의 함수값이며, 밀도를 구간에 따라 적분하면 확률이 나온다.
밀도추정은 데이터분석의 핵심적인 요소 중 하나이다.
밀도추정은 크게 Parametric 추정과 Non-parametric 추정으로 나눌 수 있다
Parametric 추정의 경우 pdf에 대한 모델을 정해놓고 데이터로 부터는 파라미터만 추정하는 방법이다.
- 예를 들어, "대한민국 연 평균 기온"이 정규분포를 따른다고 가정한 뒤 관측 데이터로 부터는 평균과 분산만 추정하는 것이다.
하지만 현실의 문제에서는 이렇게 분포를 미리 아는 경우가 많지 않기때문에 보통 Non-parametric 추정을 한다.
Non-parametric 추정은 간단하게 히스토그램을 생각하면 된다. 관측 데이터로부터 히스토그램을 구한 뒤, 이를 정규화하여 pdf로 사용하는 것이다.
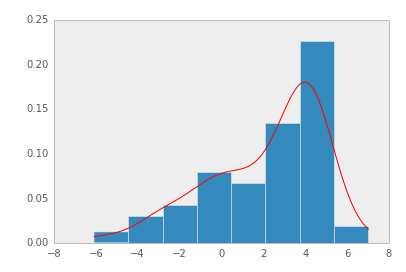
그러나, Non-parametric 밀도추정은 binary의 경계에서 불연속성이 나타나고, binary의 크기나 시작위치 등에 따라 히스토그램이 달라지며, 고차원 데이터의 경우 사용하기 힘든 문제점이 있다.
=> 이를 개선하기 위해 사용하는 것이 커널밀도추정(KDE)다.
다시 돌아와서, Parzen Windows는 이 커널밀도추정의 대표적인 방법이다.

Parzen Windows 역시 가까운 이웃을 구하는 과정을 통해 알고리즘이 진행된다.
3. Neighborhood based traing's Limitation

=> 위에서 Dimensionality Reduction(차원축소)와 Non-parametric density estimation(밀도추정)의 예시로 언급한 PCA, LDA, Isomap, LLE, parzenwindow 모두 Neighborhood based training이다.
그러나 Neighborhood based training는 고차원 데이터인 경우 지난번 포스팅에서도 언급했던것 처럼 같은 유클리디안 메소드를 사용해도 매니폴드에 따라서 실제로는 가깝지 않을 수도 있다.
=> AutoEncoder의 등장
4. 정리
이번 포스팅에서는 AutoEncoder의 특징인 Dimensionality Reduction과 Density Estimation을 하는 다른 방법을 살펴보았고, 이러한 방법들(Neighborhood based training)의 문제점에 대해서 작성해봤다.
다음 포스팅에서는 보다 더 자세히 AutoEncoder에 대해 적어보겠다.
'AI Theory > Generative models' 카테고리의 다른 글
| 최대한 쉽게 설명한 GAN (1) | 2022.02.07 |
|---|---|
| 오토인코더(Autoencoder)가 뭐에요? - 5. Variational AutoEncoder(VAE) (0) | 2022.02.03 |
| 오토인코더(Autoencoder)가 뭐에요? - 4. Practice with PyTorch (AutoEncoder) (0) | 2022.01.31 |
| 오토인코더(Autoencoder)가 뭐에요? - 3. This is AutoEncoder! (0) | 2022.01.26 |
| 오토인코더(Autoencoder)가 뭐에요? - 1.Dimensionality reduction and Maninfold Learning (0) | 2022.01.24 |




댓글