* 개인적으로, GAN에 대해 이해하기 위해서는 AE, VAE에 대한 기본적인 지식이 있어야 한다고 생각합니다. *
- References
나동빈님의 Generative Adversarial Networks (꼼꼼한 딥러닝 논문 리뷰와 코드 실습)
Naver d2 "1시간만에 GAN(Generative Adversarial Network) 완전 정복하기"
Kaist Edward Choi 교수님의 Programming for AI(AI 504, Fall2020)
0. 글 쓰기에 앞서
GAN은 최근 10년간 머신러닝 분야에서 가장 혁신적인 아이디어이다.
- 얀 르쿤
딥러닝, 그 중에서도 이미지 처리 분야에서 가장 많이 쓰이는 CNN(Convolutional Neural Network, 합성곱신경망)의 창시자 얀 르쿤(Yann LeCun)은 GAN에 대해 "적대적 학습은 가장 뛰어난 방법론이다." 라는 평가를 내렸다고 한다.
적대적 학습이란 무엇이길래 이런 극찬을 하는 것일까?
AI 504 수업에서도 GAN이 나오는데 다른 영상들을 몇개 더 참고하여 GAN에 대해 최대한 쉽고 자세하게 적어보려 한다.
1. Before GAN (사전 지식)
1-1. 이미지 데이터와 확률분포
지난번 포스팅에서 오토인코더의 매니폴드 학습에 대해 공부하다 RGB 이미지를 예시로 든 적이 있었다.
(오토인코더(Autoencoder)가 뭐에요? - 1.Dimensionality reduction and Maninfold Learning)
오토인코더(Autoencoder)가 뭐에요? - 1.Dimensionality reduction and Maninfold Learning
- Reference Naver d2 이활석님의 '오토인코더의 모든것' Kaist Edward Choi 교수님의 Programming for AI(AI 504, Fall2020) Naver d2 이활석님의 '오토인코더의 모든것'과 Kaist Edward Choi 교수님의 AI 504 수..
hyunsooworld.tistory.com
아래와 같은 200x200 RGB 이미지는 약 10^96329 개의 이미지를 표현 할 수 있다.

확률분포의 관점에서 이러한 모든 이미지 역시 다차원 공간에서 한 점으로 표현되기 때문에, 이러한 이미지의 분포를 근사하는 모델이 고차원 공간 상에 있을 것이다.
또한 사람의 얼굴 역시 통계적인 평균치가 존재 할 수 있기 때문에 모델은 이를 수치적으로 표현할 수 있을 것이다.

즉 이미지 데이터에 대한 확률 분포란 이미지에서 다양한 특징들이 각각의 확률 변수가 되는 분포를 의미한다.

1-2. 생성 모델 (Generative Models)
생성 모델은 실제로 존재하진 않지만 있을 법한 데이터(이미지, 자연어문장, 오디오)를 생성 할 수 있는 모델을 의미한다.

분류 모델의 경우 일반적으로 decision boundary를 학습하는 것이 주 목적일 것이다.
생성 모델은 각각의 class에 대해서 적절한 분포를 학습하는 것이 주 목적이다.

생성모델의 관점에서, 위 분포를 잘 학습한다면 새로운 data를 생성해 낼 수 있을 것이다.
이때, 확률이 높은 부분에서부터 noise를 섞어가며 random sampling을 한다면 그럴싸한 이미지들을 생성해 낼 수 있을 것이다.
정리하자면, 생성 모델의 목표는
"이미지 데이터의 분포를 근사하는 모델 G를 만들자"
이때 모델 G가 잘 동작한다는 의미는 원래 이미지들의 분포를 잘 모델링 할 수 있다는 것이다.
→ 대표적인 예시 : GAN(Generative Adversarial Network)
생성 모델은 다음과 같은 과정으로 원본 데이터를 학습한다.

이때 (d) 단계가 모델 G가 학습이 잘 완료된 최종 상태이다.
학습이 잘 되었다면 통계적으로 평균적인 특징을 가지는 데이터를 쉽게 생성 할 수 있을 것이다.

예를 들어, 눈의 길이와 코의 크기는 평균적인 수치를 갖게 하면서 눈썹의 길이만 길게 해서 얼굴을 만들어 낼 수도 있을 것이다.
최초의 GAN(가장 기본적인)은 이런 세부적인 feature들을 control하진 못했지만 이후에 GAN과 관련된 다양한 논문들이 나오면서 가능해졌다.
2. GAN (Generative Adversarial Network)
2-1. GAN의 의미
그렇다면 본격적으로 GAN에 대해서 알아보자.
GAN은 실제로는 존재하지 않지만 현실에 있을법한, 그럴싸한 이미지를 만들 수 있는 생성 모델의 한 종류이다.
GAN을 설명할 때 가장 이해하기 쉬운 예시는 경찰과 위조지폐범 예시다.
위조지폐범은 경찰이 위조지폐를 구분하지 못하도록 진짜 지폐 같은 가짜 지폐를 만드는 것이 목적이다.
반면, 경찰은 위조지폐범이 생성한 지폐를 진짜인지 가짜인지 구분해야한다.
경찰이 점점 지폐를 잘 구분한다면 위조지폐범은 더 그럴싸한 위조지폐를 만들어야하고, 이렇게 둘은 서로 자신의 목적을 달성하기 위해 진화(학습)한다.
GAN은 생성자(generator,위조지폐범)과 판별자(discriminator,경찰) 두 개의 네트워크를 활용한 생성 모델이다.
GAN에서 Adversarial(적대적인)이라는 단어가 붙은 이유는 바로 이 때문이다.
학습이 완료된 후 우리가 사용하는 모델은 생성자(generator)이고 판별자(discriminator)는 생성자의 학습을 도와주는 역할을 한다.
2-2. GAN의 목적함수
GAN은 아래의 목적함수를 통해 이미지 분포를 학습한다.
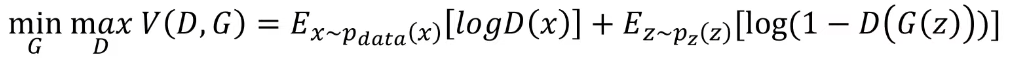
목적함수를 해석해보면, 임의의 함수 V가 있을 때 V는 D(판별자)와 G(생성자)로 이루어져있다.
이때 G는 함수 V를 minimize(낮추려고)하고 D는 maximize(높이려고)한다.
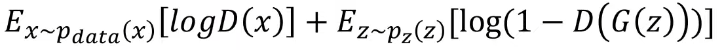
- Ex~pdata(x)[logD(x)] 부분은 원본 data에서 x를 sampling해서 D에 넣고 log를 취해서 평균을 구한 값이다.
- 이때 pdata는 원본 data의 분포를 의미한다.
- Ez~pz(z)[log(1-D(G(z)))] 부분에는 생성자(G) 개념이 포함되어있다.
- 일반적으로 생성자(G)는 noise vector로 부터 입력을 받아서 새로운 이미지를 만들 수 있는데 pz(z)는 바로 이 noise를 sampling 할 수 있는 분포다.
- 이런 분포(pz(z))에서 random한 noise z를 sampling하고 이를 생성자 G에 넣어서 가짜 이미지 G(z)를 만들고, 그 가짜 이미지를 다시 D에 넣고 1에서 그 값을 뺀 후 log를 취해주고 평균을 구한 것이다.
설명이 난해하지만 식과 비교하며 차근차근 읽어보면 이해가 될 것이다..
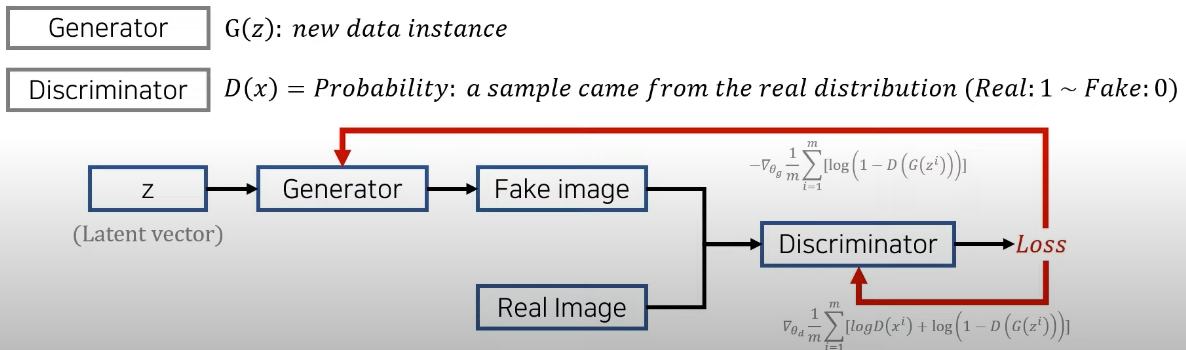
Generator는 하나의 noise vector인 z를 받아서 새로운 이미지 instance를 만들 수 있고, Discrimiator는 이미지 x를 받아서 그 이미지가 얼마나 진짜같은지에 대한 확률값을 출력으로 내보낸다. (Real: 1 ~ Fake: 0)
- Discriminator의 입장에서는 원본 데이터 x에 대해서는 1을 출력하고, 가짜 데이터 G(z)에 대해서는 0을 출력할 수 있도록 학습을 진행하는 것이다.
- Generator의 입장에서는 자기가 만든 가짜 이미지가 판별자에 의해서 진짜라고 인식이 되도록(D가 1을 출력하도록) 학습을 진행한다. 즉, 그럴싸한 가짜 이미지를 생성하는것이 목적이다.
GAN은 인공신경망(Network)을 활용해 두 개의 모델(생성자, 판별자)을 적대적(Adversarial)으로 경쟁시키며 발전하는 생성 모델(Generative)이다.
=> Generative Adversarial Network
2-3. GAN의 수렴과정
그렇다면 위에서 나온 목적함수를 어떤 과정으로 이용해 학습을 진행할까?
GAN의 수렴과정을 자세히 살펴보면서 위 질문에 대한 답을 해보겠다.
우선 GAN의 목표는 두가지 이다.
- Pg → Pdata : 생성자의 분포가 원본 학습 데이터의 분포를 잘 따른다.
- D(G(z)) → 1/2 : 학습이 끝난 후에는 가짜 이미지와 진짜 이미지를 구분할 수 없어야한다. (항상 output이 1/2)
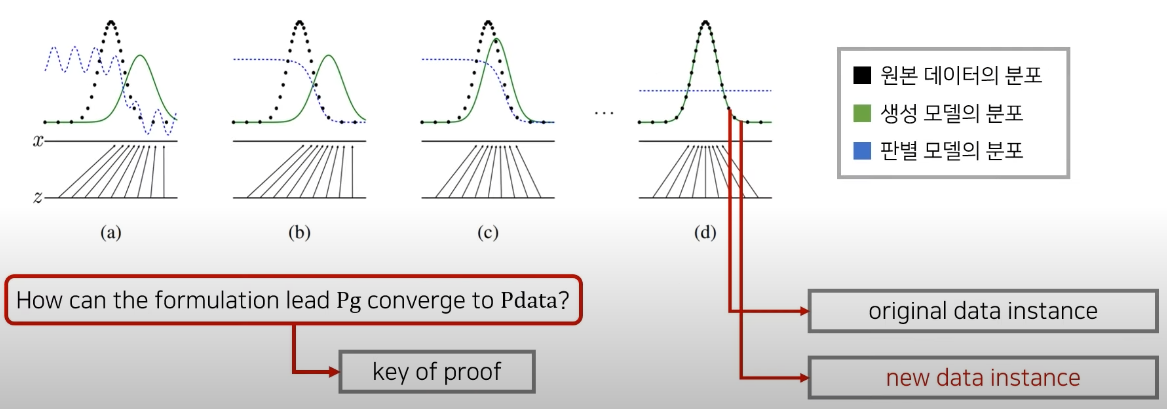
파란색 점선인 판별 모델의 분포를 보면 처음에는 잘 판별을 하다가(Real: 1 ~ Fake: 0), 학습이 진행 될 수록 1/2로 수렴하는 형태가 된다.
How can the formulation lead Pg converge to Pdata?
학습을 진행할 때 왜 생성자의 분포(Pg)가 원래 분포(Pdata)로 수렴하나?
=> 이 질문에 대한 답변이 GAN의 핵심이다.
이를 증명하기 위해서는 우선 Global Optimality에 대한 증명이 필요하다.
매 상황에 대해 생성자와 판별자가 어떤 포인트로 Global Optima를 갖는지 살펴보자.
Global Optima란 특정 파라미터가 모든 경우(global)를 통틀어 최적(optima)인 경우를 의미
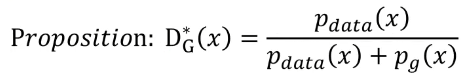
만약 G가 고정이라면, 다음과 같은 과정으로 목적함수를 변형 할 수 있다.
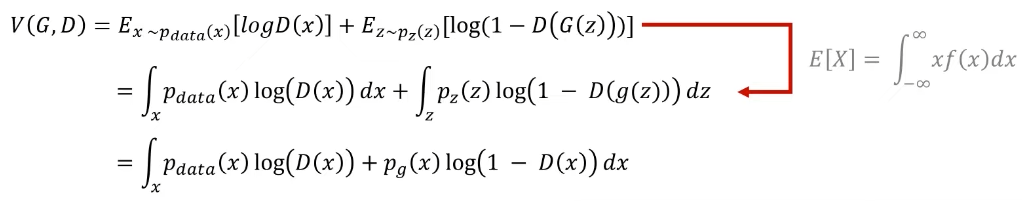
2번째 식에서 3번째 식으로 넘어 갈 수 있는 것은 z domain에서 sampling 된 noise vector를 g에 넣어서 데이터 x를 만들어 낼 수 있기 때문에 (즉, z에서 x로 mapping 가능) x로 치환하면 가능하다.
결국 목적함수는 다음과 같이 나타낼 수 있다.
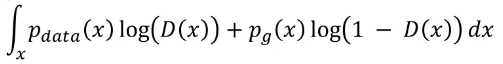
이때, f(y) = alog(y) + blog(1-y) 는 [0,1]에서 a/(a+b)일때 y가 극댓값을 갖는다는 성질이 이미 증명되어있다.
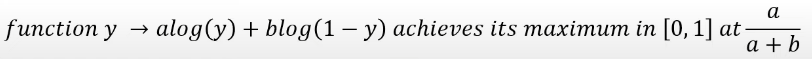
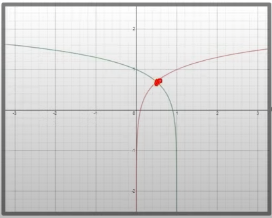
즉, 처음 가정한 명제가 성립할 때 목적함수의 적분식이 최대가 되는것이다.
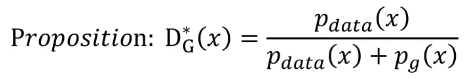
그렇다면 이제 궁극적으로 아래 명제에 대해 증명을 해보자.
(How can the formulation lead Pg converge to Pdata?에 대한 답변)
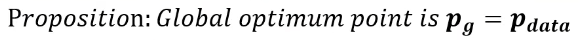

우선 새로운 함수 C(G)를 정의한다.
이때 C는 V(G, D)를 최대로 만드는 D에 대한 V 함수다. (D의 global optima는 바로 위에서 구했다.)
이후 log의 성질을 이용해 + log(2) + log(2) - log(4)를 해준다(+log(2)는 기댓값 term의 분자를 2배 해준 것과 같다.)
바꿔주는 이유는 증명의 편의성 때문인데(JSD를 사용하기 위해), 우선 각각의 기댓값 term들을 KLD로 치환 해보자.
쿨백-라이블러 발산(KLD,Kullback–Leibler Divergence)에 대한 자세한 설명은 오토인코더(Autoencoder)가 뭐에요? - 5. Variational AutoEncoder(VAE) 에서 볼 수 있다. 간단히 설명하면 KLD는 두 분포가 얼마나 차이가 있는지 측정하는 수치다.
오토인코더(Autoencoder)가 뭐에요? - 5. Variational AutoEncoder(VAE)
- Reference Naver d2 이활석님의 '오토인코더의 모든것' Kaist Edward Choi 교수님의 Programming for AI(AI 504, Fall2020) Naver d2 이활석님의 '오토인코더의 모든것'과 Kaist Edward Choi 교수님의 AI 504 수..
hyunsooworld.tistory.com
KLD은 distance metric(거리 측정법)으로 활용하기는 어렵기 때문에 JSD를 이용해야한다.
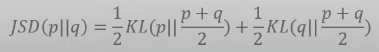
JSD(Jensen–Shannon divergence)는 두 확률 분포 사이의 유사성을 측정하는 방법이다.
이는 KLD의 두 분포의 순서를 바꿔서 구하고 그것을 평균낸 값이다.
(이렇게 하면 기존에 거리 개념으로서 사용 할 수 있다)
이때 JSD는 distance metric이기 때문에 두 분포가 똑같을때 최솟값이 0이 된다.
따라서 Pdata와 Pg가 동일할 때 (Pdata=Pg), 최솟값인 0 이 되고 결국 C(G)의 최솟값은 -log(4)가 된다.
지금까지 한 증명은 D가 이미 잘 수렴한 상태에서 (gloabl optima를 가지고 있는 상태) 생성자가 잘 학습된다면
-log(4)와 같은 최솟값을 가질 수 있을 것이라는 내용이다.
이 증명은 생성자와 판별자 각각에 대해서 global optimum point가 존재 할 수 있다는 내용을 증명한 내용이고,
학습이 잘 되어서 이러한 global optima에 잘 도달할 수 있는가 에 대한 내용은 엄밀히 다른 내용이다.
초기의 GAN 논문에서는 자세하게 언급하고 있지는 않지만, 이후 논문들에서 학습의 안정성을 더할 수 있는 다양한 테크닉들이 나왔다.(한마디로 나중에 더 알아보자)

2-4. GAN을 활용한 이미지 생성

GAN을 활용해 만든 이미지들은 다음과 같은 특징을 갖고 있다.
- Not cherry-picked : 별도로 선별 x , random하게 넣은 것
- Not memorized the training set : 노란 박스는 그 바로 왼쪽 데이터와 최대한 가까운 학습 데이터를 의미한다.
- Competitive with the better generative models : 다른 생성 모델과 비교했을 때 충분히 좋은 성능이 나온다.
- Images represent sharp : AE계열의 다른 생성 네트워크와 비교했을때, blurry 하지 않고 sharp한 이미지가 나온다.

위의 예시를 보면 1에서 5로 변할때 있을 법한 이미지들을 거치면서 자연스럽게 변하는 것을 볼 수 있다.
생성자에 들어가는 latent space의 공간에서 만들어지는 이미지들은 각각 그럴싸한 이미지로 변형 될 수 있음을 보여준다.
3. 정리
이번 포스팅에서는 GAN의 개념과 목적함수를 통해 GAN이 어떠한 과정으로 학습을 진행하는지에 대해 정리해봤다.
다음 포스팅에서는 pytorch를 이용해 직접 GAN을 구현해보는 코드를 정리해볼 것이다.
'AI Theory > Generative models' 카테고리의 다른 글
| 생성모델의 평가지표 톺아보기(Inception, FID, LPIPS, CLIP score, etc ..) (4) | 2024.02.07 |
|---|---|
| 오토인코더(Autoencoder)가 뭐에요? - 5. Variational AutoEncoder(VAE) (0) | 2022.02.03 |
| 오토인코더(Autoencoder)가 뭐에요? - 4. Practice with PyTorch (AutoEncoder) (0) | 2022.01.31 |
| 오토인코더(Autoencoder)가 뭐에요? - 3. This is AutoEncoder! (0) | 2022.01.26 |
| 오토인코더(Autoencoder)가 뭐에요? - 2.Why AutoEncoder? (0) | 2022.01.25 |




댓글