오토인코더(Autoencoder)가 뭐에요? - 5. Variational AutoEncoder(VAE)

- Reference
Naver d2 이활석님의 '오토인코더의 모든것'
Kaist Edward Choi 교수님의 Programming for AI(AI 504, Fall2020)

Naver d2 이활석님의 '오토인코더의 모든것'과 Kaist Edward Choi 교수님의 AI 504 수업을 토대로 공부한 후 정리하였습니다.

0. 글 쓰기에 앞서

지난번 포스팅에서는 MNIST data를 가지고 AutoEncoder 실습코드를 구현해봤다.

이번 포스팅에서는 Variaitional AutoEncoder이란 무엇이고 AutoEncoder과 어떻게 다른지, 또 언제 쓰이는지 알아보자.

(내용이 정말 어렵고 ,, 많고 ,, 어렵다!)

(지난번 포스팅 -> 오토인코더(Autoencoder)가 뭐에요? - 4.Practice with PyTorch (AutoEncoder)

오토인코더(Autoencoder)가 뭐에요? - 4. Practice with PyTorch (AutoEncoder)

1. VAE(Variational AutoEncoder란?

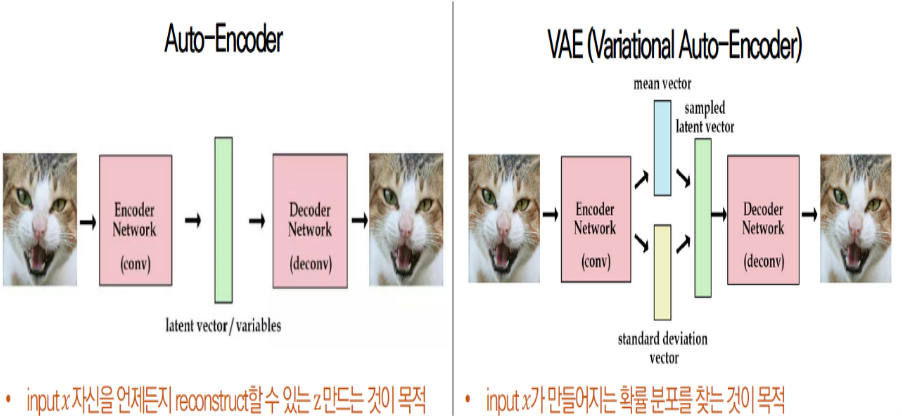
1-1. AE vs VAE

앞에서 AutoEncoder는 그 목적이 manifold를 학습하는 것이라고 배웠다. (Encoding(앞쪽) 부분)

반면, Variational AutoEncoder의 목적은 generate model learning 즉 데이터를 생성하는 것이다. (Decoding(뒷쪽) 부분)

따라서 AutoEncoder와 Variational AutoEncoder는 목적부터 완전 다른, 서로 연관성이 없는 개념이다.

그러나 그 구조를 보니 공교롭게도 서로 비슷한 구조를 이루고 있어 코드로 비교해보면 거의 차이가 없다.

AE(좌) vs VAE(우)

1-2. Generative model

Generative Model의 구조

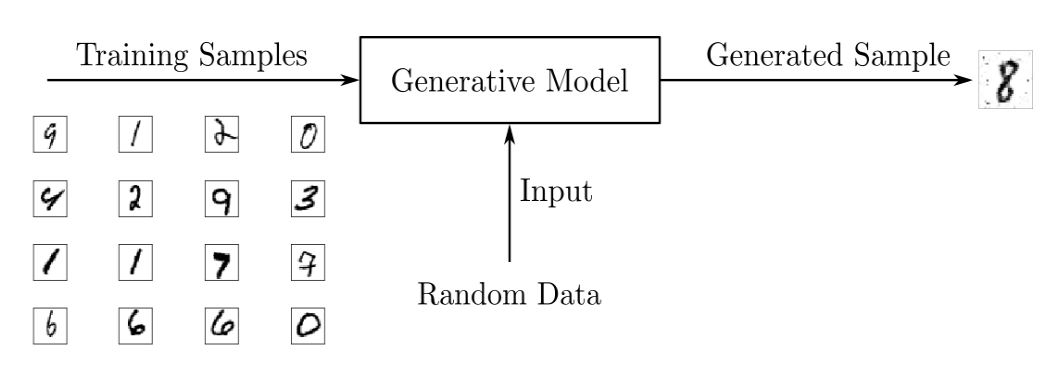
VAE는 Generative Model이다

그렇다면 Generative Model은 무엇일까?

Generative Model은 training data가 주어졌을 때,

이 training data가 가지는 real 분포와 같은 분포에서 sampling된 값으로 new data를 생성하는 model을 의미한다.

 

결국 우리가 알고 싶은것은 p(x) (모든 training db에 대한 확률분포)

 이때 Z는 입력 값으로 들어가는데, generator이 이미지를 만들어 낼 때 랜덤하게 만들어 내는 것 보다는 만들어진 이미지를 control하면 더 좋을 것이다.

ex) 사람 얼굴을 생성하는 model이 있을 때 무작정 랜덤한 얼굴을 생성하는 모델보다, 성별이나 스타일등을 control 할 수 있는 모델이 더 좋을 것이다.

Z는 remote controller로서 이해하면 될 것이고, 그러므로 다루기 쉬운 확률분포를 사용한다(gaussian distribution, uniform distribution)

 

그렇다면 여기서 이런 질문을 할 수 있을 것이다.

 

Manifold가 굉장히 복잡한 고차원 공간이라면, 단순한 Z(gaussian ,uniform)의 분포를 sampling 한다고 해서 그 공간을 잘 설명하거나 찾을 수 있을까?

 

 

정답은 가능하다.

이유는 학습을 수행하는 네트워크가 deep neural network이기 때문이다.

실제로 우리가 배워야되는 manifold가 복잡하다 하더라도 앞의 한 두개 layer정도는 그 복잡한 manifold를 잘 찾기 위한 역할을 수행 할 수 있다.

위 사진의 우측 그림과 같이 정규분포를 따르는 Z를 한번만 변형시켜줘도 원형의 분포를 뽑아낼 수 있다.

따라서 prior distribution은 간단한 분포를 사용해도 걱정하지마라!!

 

또 이런 의문도 들 수 있습니다.

그럼 MLE(Maximum Likelihood Estimation)를 바로 사용하면 안되나?

답은 안된다이고, MLE를 사용하면 안되기 때문에 우리는 Variational AutoEncoder를 사용하는 것이다.

이유를 간단하게 말하면 데이터가 MSE 관점에서 가깝다고 실제 의미적으로도 가까운 것은 아니기 때문이다.

(c)는 (a)를 우측으로 몇 픽셀 이동시킨 것이고, (b)는 (a)의 일부를 훼손시킨 것이다.

위 사진에서 (a)와 (c)는 의미론적으로 같은 이미지이다.

이때 MSE(MeanSquaredError)를 구해보면, (a)와 (c) 사이의 MSE가 (a)와 (b) 사이의 MSE보다 훨씬 크다.

 

우리의 목표는 p(x)의 likelihood값을 높이는 것이다. (그래야 sampling했을 때 p(x)가 나올 확률이 높다)

만약 conditional probability를 가우시안이라고 가정한다면 (가우시안 가정은 MSE로 likelihood 값을 정해준다),

(a)의 likelihood는 평균값이 (b)일때 크다.(사실 (c)일때 커야함)

따라서 이렇게 학습된 모델에서 sampling을 할 경우 (c)가 나올 확률보단 (b)가 나올 확률이 더 크다.

 

결론

우리는 p(x)의 likelihood값이 높기를 바란다.

이때 likelihood값을 결정하는 가우시안 분포에서 평균에 해당되는 x가 MSE관점에서 작은 값이 선택이 되는데, 이때 선택된 값이 실제 우리가 의미적으로 생각했을 때 나와야할 값이 아니라는 것이다

따라서 우리는 위 식에서 p(z), sampling 함수를 신경써야한다.

=> Variational Auto Encoder의 등장

 

1-3. VAE의 IDEA

위의 내용들을 짧게 요약하자면 다음과 같다.

1. prior에서 sampling했더니 학습이 잘 안됨 (나와야 할 이미지가 안나오고 이상한 이미지(b)가 나옴)
2. prior에서 sampling하면 안되겠다 (MSE 말고 VAE를 사용하자)
3. p(z|x) 즉 evidence인 x가 주어진 이상적인 sampling 함수에서 sampling 해보자!

🔎 VAE의 IDEA

Generator를 학습할때 그냥 시키면 학습이 잘 안되므로 (학습이 잘 되기위한) z sample을 잘 만들어내는 이상적인 sampling 함수를 찾아보자. variatioal inference 방법으로 우리가 알고있는 확률분포approximation class를 target distribution(true posterior)과 제일 가깝게 만든 후 그 분포를 이용해 sampling하고 generator를 학습시키면 잘 될것이다.

variational inference method

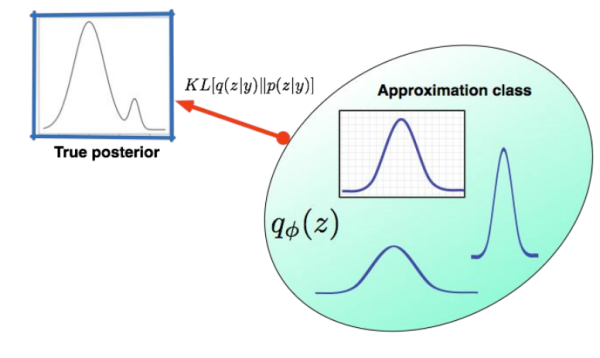
Variational inference란 approximation class(known, ex: gaussian)의 파라미터를 바꿔가며 true posterior(unknown)에 가깝게 만드는 것이다.

그리고나서 이때 사용한 approximation class를 이용해 sampling을 하면 x가 잘 생성될 것이다.

 

target distribution(true posterior)를 p, approximation class를 q라고 하면 p와 q의 분포가 최대한 가까워야 하는데,

이때 사용하는 것이 쿨백-라이블러 발산(KLD,Kullback–Leibler Divergence)이다.

 

1-4. 쿨백-라이블러 발산(KLD,Kullback–Leibler Divergence)

쿨백-라이블러 발산(KLD,Kullback–Leibler Divergence) : P분포와 Q분포가 얼마나 다른지 측정하는 지표

KLD는 그 값이 낮을수록 두 분포가 유사하다고 해석하며 값은 항상 양수다.

KLD는 P와 Q의 계산 순서가 바뀌면 값이 변함(거리 개념 x)

 

그렇다면 수식을 통해 KLD가 어떻게 나오는지 알아보자

KLD의 유도과정

KLD와 ELBO는 trade-off 관계 (하나가 증가하면 하나는 감소)

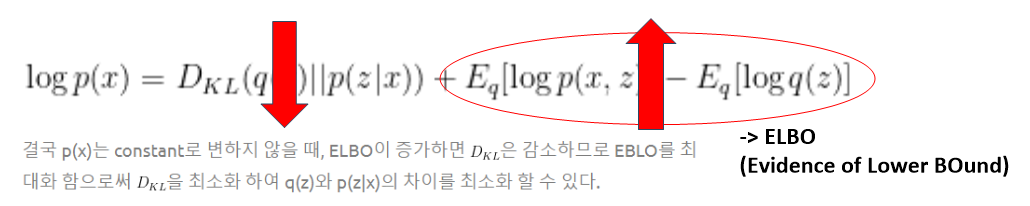
log(p(x))를 정리하다보면 log(p(x))는 결국 ELBO와 KLD의 합임을 알 수 있다.

즉, KLD를 최소화 해야하는데 p(z|x)를 모르고 p(x)는 고정이기 때문에 ELBO 값을 최대화 함으로서 KLD를 최소화 할 수 있는 것이다.

 

1-5. ELBO : Evidence LowerBOund

KL을 minimize하는 것과 ELBO를 maximize하는 것은 같은 얘기다.

ELBO를 정리해보면 KL이 다시 나오는데 이는 앞에서 나온 KL과 다르다.

 

식 전체를 정리해보면 다음과같은 수식을 얻을 수 있다.

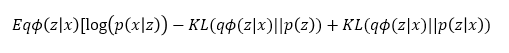
위 수식에서 각 term들이 어떤 의미를 가지고 있는지 이해하는 것이 가장 중요하다.

출처 : https://deepinsight.tistory.com/127?category=842339

이때 두 확률분포 사이의 거리를 나타내는 KL term은 우리가 계산 할 수 없으므로 ELBO를 maximize 해줘야한다.

ELBO는 다시 Reconstruction term 과 Regularlization term으로 나뉘므로 이를 최적화 시켜주는 것이 핵심이다.

 

 

우리가 optimize 해야할 두가지 문제

결국 해결해야 할 optimization problem은 Variational Inference(on Φ) , Maximum likelihood(on θ) 이렇게 두가지다.

이 두가지 문제를 하나의 식으로 정리하면 다음과 같다.

ELBO를 \(\phi\)에 대해 maximize하면 variational inference(문제1)이 되고, \(\theta\)에 대해 maximize하면 maximum likelihood(문제2)가 된다.

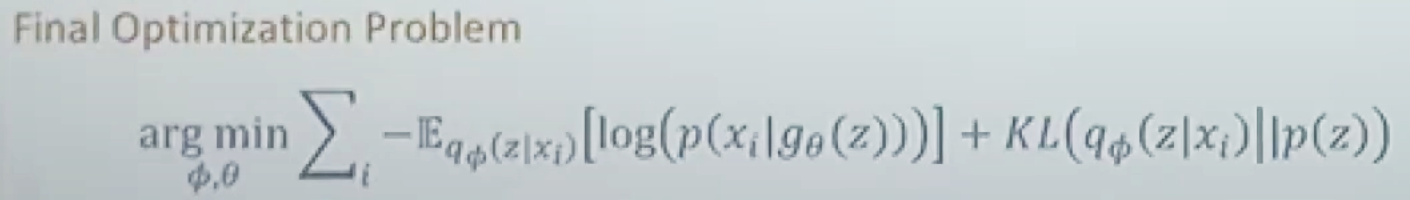
VAE는 AE의 구조를 가지면서(input, output이 x로 동일), variational inference 방법을 사용하기 때문에 Variational Auto Encoder (VAE) 인 것이다.

The mathmatical basis of VAEs actually has relatively little to do with classical autoencoders. (VAE와 AE는 관계가 없다)

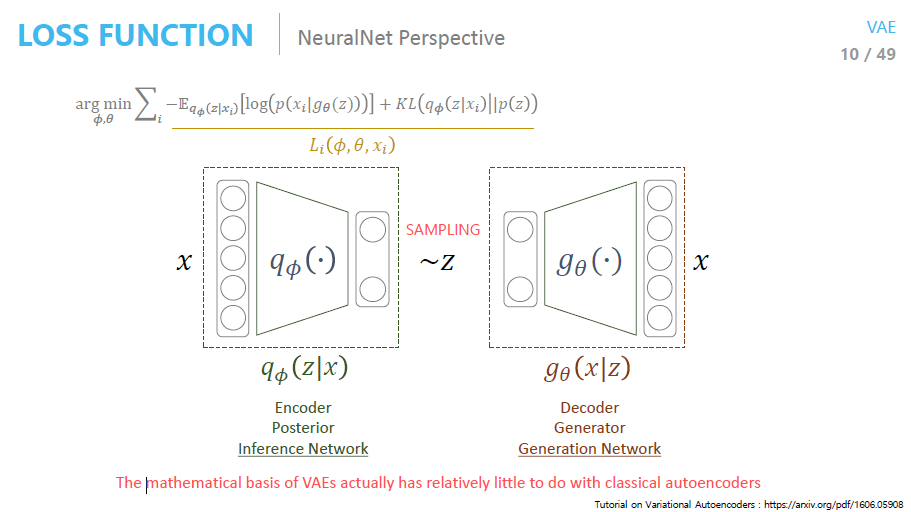
1-6 . VAE 흐름 정리

내가 이해한 VAE의 흐름은 다음과 같다.

우리의 목표 : Generator 학습

prior에서 학습을 시켰더니 학습이 잘 안된다.
↓
이상적인 함수(x를 evidence로 주고, x에 대해서는 잘 geneation되는 함수)에서 학습을 시키자.

↓
이상적인 함수는 뭔데?

↓
잘 모르니까 approximation하는 q(\(\phi\))함수를 찾는다.

↓
어떻게 q(\(\phi\))함수를 찾나?

↓
ELBO term을 \(\phi\)에 대해서 maximize하면 됨 (variational inference 방법)

↓
찾은 q(\(\phi\))함수로 부터sampling 해서 나온 값이 x가 될 확률을 maximize하고 싶다(MLE 추정)

↓
MLE 추정은 어떻게?

↓
ELBO term의 앞부분이므로 \(\theta\)에 대해 maximize하면 MLE가 된다.

 

 

2. 조금 더 자세히

2-1. ELBO를 더 자세히

ELBO term을 조금만 더 자세히 봐보자.

Reconstruction Error term에서 기댓값을 구할때 적분 대신 몬테카를로 방법을 이용해 샘플링을 한 후 평균을 구한다.

이때, sampling을 할때 한가지 문제가 발생한다.

Backpropagation은 chain rule을 사용해 편미분을 계속 해줘야하는데, mu와 sigma가 계속 랜덤으로 바뀐다면 chain rule을 쓸 수가 없다.

Reparameterization Trick(우측식으로의 변형)을 통해 backpropagation을 가능하게 한다.

Reparameterization Trick을 사용해도 분포는 변하지 않고, 이로부터 \(\mu\)와 \(\sigma\)에 대한 그래디언트를 구할 수 있다.

Reparameterization Trick : \(\mu\)과 \(\sigma\)는 고정시키고 \(\epsilon\)만 정규분포에서 sampling 해준다.
=> 확률적 특성은 서로 같다 (이미 증명됨)

mu와 sigma는 tf.random_normal을 하지 않는다. (Reparameteriztion trick)

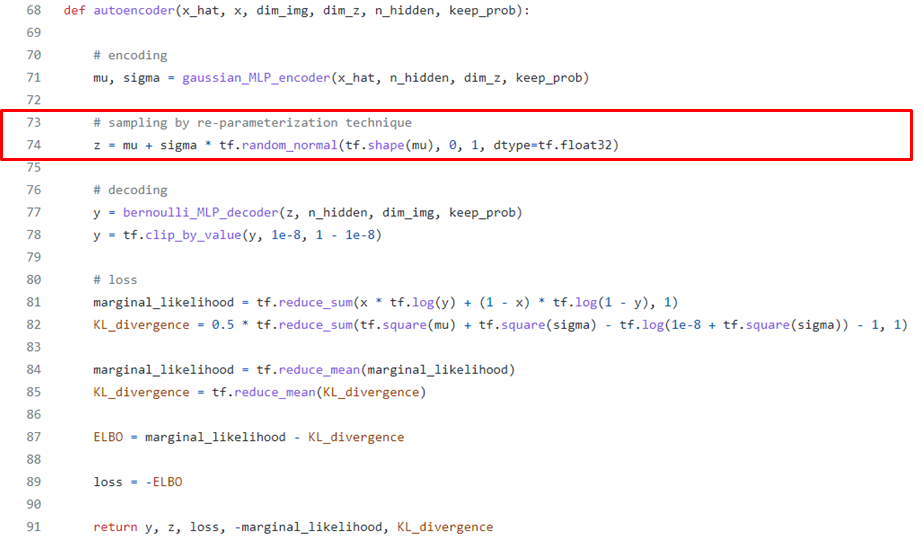
2-2. Bernoulli Decoder? Gaussian Decoder?

또한, 몬테카를로 방법을 사용할 때 단 한번만 샘플링(L=1)을 해서 사용한다.

따라서 우리는 아래의 loglikelihood 값만 계산하면 reconstruction error term을 계산 할 수 있는 것이다.

구해야하는 loglikelihood

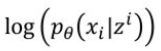
loglikelihood를 계산하려면 우선 conditional probability를 정해야된다.

보통 conditional probability는 대표적으로 Bernoulli와 Gaussian 등이 있고, 이미지 분야에서는 주로 Bernoulli를 따른다고 가정한다.

 

Bernoulli를 가정하고 식을 정리해보면 결국 loglikelihood는 input x와output p의 Cross-entropy가 됩니다.

Cross-entropy라고 무조건 output의 label이 one-hot encoding으로 0과 1의 값만 가지는 것은 아니다(softmax).

 

그렇다면 여기서 만약 conditional probability를 Bernoulli가 아닌 Gaussian으로 가정하면 어떻게 될까?

conditional probability를 Gaussian으로 가정

likelihood pθ​(x∣z)는 input x와 output μ(를 따르는 샘플) 간의 MSE loss가 된다.

특히, 분산을 1로해서 \(\mu\)만 추정했을 때에 완벽한 MSE loss가 된다.

만약 학습이 잘 됐다면 z를 q\(\phi\)​(z∣x)에서 샘플링했음에도, 이상적인 p(z∣x)와 굉장히 비슷할 것이다.

또한 샘플링한 z를 토대로 generator q\(\theta\)​​(x∣z) 또한 최적화된 것이기 때문에 생성 성능이 좋을 것이다.

 

VAE의 코드를 보면 decoder에서 conditional probability의 가정이 Bernoulli인지 Gaussian인지에 따라 내용이 다르다.
→ 굉장히 헷갈림!

2-2-1. Case1 : Gaussian Encoder + Bernoulli Decoder

Autoencoder의 구조 (Gaussian Encoder+Bernoulli Decoder)

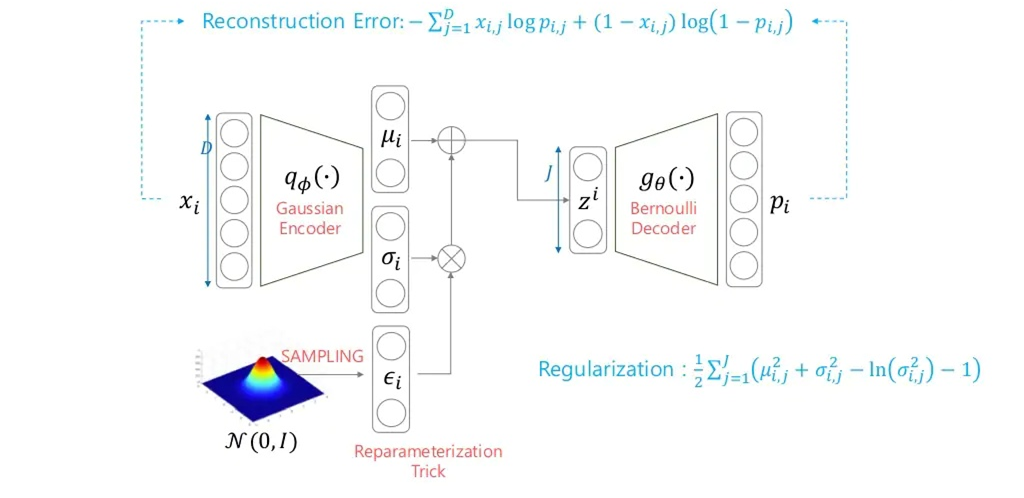
1. prior를 통해 sampling하면 잘 안되니 x를 evidence로 주고 sampling 함수를 찾자.
2. (sampling 함수가 Gaussian이라는 가정하에) sampling 함수를 찾으려면 \(\mu\)와 \(\sigma\)를 찾는다.
3. 그 후 sampling을 진행하는데 이때 reparameterization trick을 사용한다.(정규분포에서 \(\epsilon\) sampling 후 \(\sigma\)와 element wise 곱(요소별 곱셈)을 해준 후 \(\mu\)를 더해준다.
4. 그 값을 Decoder에 넣어줘서 출력값을 계산해야하는데 decoder이 Bernoulli라고 가정하면 decoder의 output과 encoder(gaussian)의 input값이 Cross-entropy 형태로 나온다.
5. KL-term(Regularization term)은 q\(\phi\)와 prior과의 관계(두 분포가 얼마나 다른지)이고 prior이 normal distribution이라고 했기때문에 closed form으로 정확한 해를 계산할 수 있다.

 

2-2-2. Case2 : Gaussian Encoder + Gaussian Decoder

Autoencoder의 구조 (Gaussian Encoder+Gaussian Decoder)

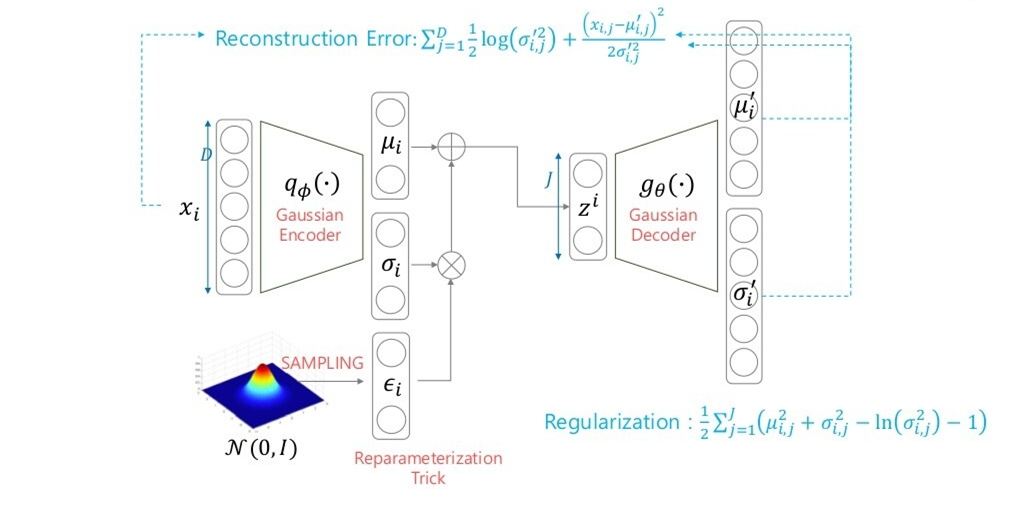
만약 Decoder부분의 conditional probability를 Gaussian으로 가정한다면 Regularization term은 바뀌지 않는다. Reconstruct Error만 바뀐다.

 

2-2-2 Case3 : ??? Encoder + Decoder → Adverarial Auto Encoder의 등장

앞의 두 케이스에서는 Decoder 부분의 conditional probability 가정만 변화를 주었다.그 이유는 Encoder 부분에서 정규분포(Gaussian)이 아닌 다른 분포의 경우 KL-term을 계산하기가 매우 어렵기 때문이다.

이를 해결하기 위해 나온것이 바로 AAE(Adversarial Auto Encoder)이다.

(AAE(Adversarial Auto Encoder)에 대해서는 추후에 포스팅하도록 하겠습니다.)

 

 

3. Result (with MNIST)

Reconstruction 관점에서의 성능 : 학습이 잘 됐으면, reconstruction-loss가 작을 것이다

즉, input : x → output : x

3-1. Reproducing

z는 몇 차원으로 줄였는지를 의미

위 사진은 MNIST 데이터에서 Input image에 따른 reproducing 결과를 나타낸다.

이때, z는 기존의 28*28(784) 차원의 이미지를 몇 차원으로 줄였는지를 의미하는데, 당연히 z값이 작을수록 더 작은 차원으로 줄였다는 것이고 그만큼 복원하기가 더 어려울 것이다.

 

3-2. Denoising

VAE에서 input값에 noise를 추가한 경우)

output은 noise 추가하기 전 input값과 동일해야한다.

거의 대부분 잘 복원한 것을 알 수 있다.

(Denosing 효과가 매우 탁월하다)

 

3-3. AE vs VAE (Data generation 관점)

AE는 데이터 압축이, VAE는 데이터 생성이 목적이다.

AE와 VAE는 코드 관점에서 딱 한 줄 다르다. (KL-term)

데이터 생성 관점에서, KL-term의 유무는 굉장히 큰 차이가 있다.

AE는 prior에 대한 조건이 없기 때문에 z의 범위가 계속 바뀐다. 즉 새로운 이미지를 생성할 때마다 z 값이 계속 바뀌게 된다.

VAE는 prior에 대한 조건이 있기 때문에 z와 prior이 같은 분포를 따른다. 따라서 z를 sampling 할때 그냥 prior에서 sampling하면 된다.

KL-term의 역할(매니폴드의 위치가 안정적이게됨)

VAE를 통해 학습시킨 MNIST data

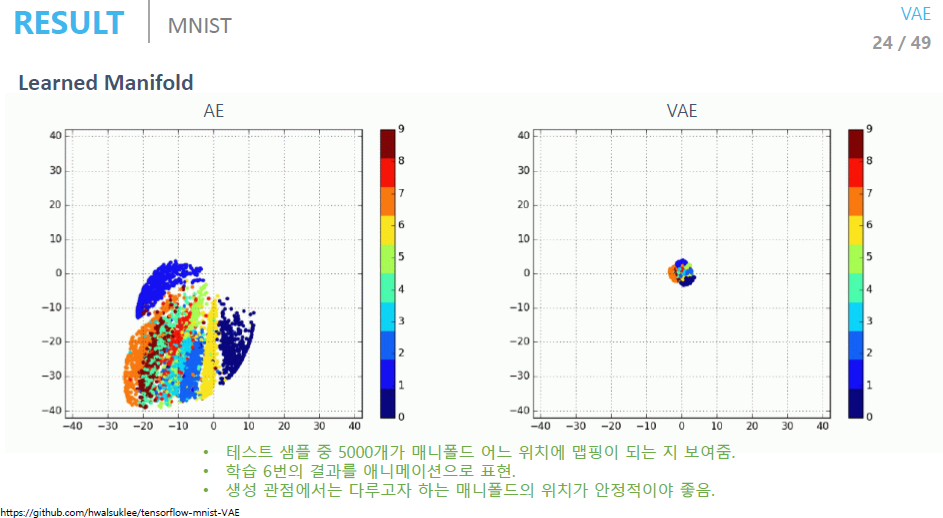
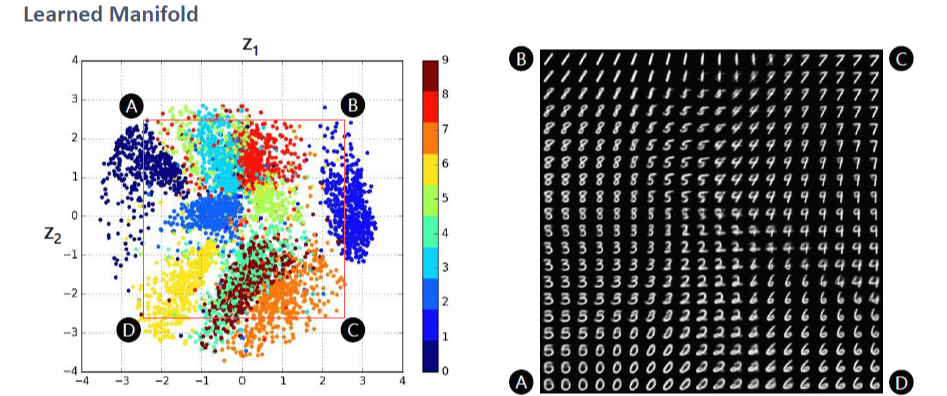
VAE를 통해 학습을 잘 진행하였다면, 2D공간에서 같은 숫자들을 생성하는 z들은 뭉쳐있고, 다른 숫자들을 생성하는 z들은 떨어져 있을 것이다. 또한 z vector는 데이터의 중요한 특징들을 포함하고 있다. (자동으로 feature 생성)

 

4. 정리

이번 포스팅에서는 VAE에 대해 자세하게 살펴보았다. 사실 굉장히 어려운 내용이라 정리하는데도 굉장히 오래걸렸다.

원래는 CVAE와 AAE도 한번에 정리하려했는데, VAE를 완벽하게 이해하고 나서 다음 포스팅에서 따로 정리해야겠다.