해당 포스팅의 모든 자료는 CS224W 강의 및 관련 자료를 바탕으로 정리하였습니다.
0. 들어가기에 앞서
경쟁력 있는 AI 개발자가 되기 위해서는, 다양한 딥러닝 학습 방법론을 바탕으로 주어진 데이터에 적합한 메소드를 구현해나가는 능력이 필수적이다.
시계열 데이터에서는 물론 네이버 부스트캠프에서 공부하고 있는 자연어처리까지 다양한 분야에서 GNN(Graphical Neural Network)이 활용되고 있고, 꼭 한번은 이 분야를 공부해보고 싶었었는데 좋은 기회로 스터디에 참여하게 되었다.
이번 주 부터는 Stanford CS224W: Machine learning with Graph 강의를 보고 관련 내용을 정리해 나갈 것이다.
1. Why Graphs
Why Graphs?
- Graphs are a general language for describing and analyzing entities with relations/interactions.
즉, 그래프(Graph)는 여러 데이터들의 관계/상호작용 등을 나타내는 효과적인 도구인데, 이는 아래와 같은 다양한 분야의 데이터를 표현하는데 사용되기 때문에 이에 대한 이해가 반드시 필요하다.



Main Quesition (for this class)
- Q : How do we take advantage of relational structure for better prediction?
- A : By explicitly modeling relationships we achieve better performance!
그래프를 통해 데이터들의 관계를 명시적으로 더 잘 모델링 할 수 있다면, 이는 더 좋은 성능으로 이어질 것이다.

Graphs(Networks)는 Image나 Text와 같은 일반적인 데이터들에 비해 구조가 더 복잡하기 때문에 처리하기가 어렵다.
이미지나 텍스트 처럼 그 크기나 방향(상,하,좌,우) 등이 정해져있지 않기 때문에 spatial locality를 가지면서도 이를 표현하기는 어려운 것이다.
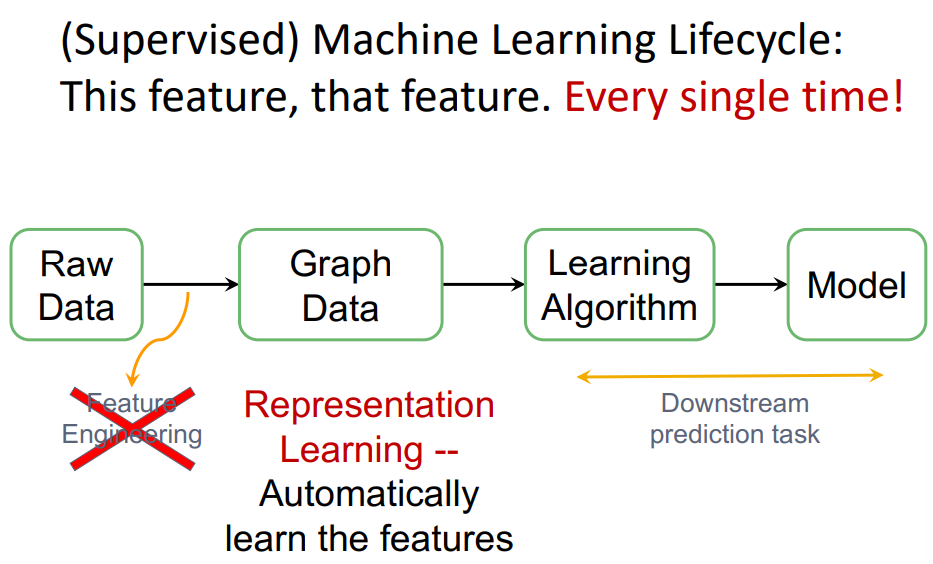
Graph를 통해 우리는 머신러닝에서 feature engineering에 해당하는 부분을 자동으로 해결할 수 있고, 데이터의 구조 역시 더 쉽게 파악할 수 있다.
이 수업에서는 features를 자동으로 학습하는 Representation Learning에 대해 집중적으로 배울 것이다.

전통적인 방법론인 Graphlets, Graph Kernels부터 그래프의 node embedding 방법, GNN 계열의 모델들(GCN, GAT 등등), 실제 산업에 적용(추천시스템, 바이오 등) 등에 대한 내용을 다룰 것이다.
2. Applications of Graph
Graph와 관련한 다양한 task들은 여러 타입으로 분류할 수 있다.

Graph level, Node level, Community level, Edge level 등으로 분류된다.
전통적인 Graph Machine Learning Tasks에는 다음과 같은 종류가 있다.
- Node classification : Predict a propery of a node
- Categoize online users / items
- Link prediction : Predict whether there are missing links between two nodes
- Knowledge graph completion
- Graph classification : Categorize different graphs
- Molecule property prediction (분자 특성 예측)
- Clustering : Detect if nodes form a community
- Social circle detection
- Other tasks
- Graph generation : Drug discovery
- Graph evolution : Physical simulation
이러한 task들은 단백질의 아미노산 구조 예측, 다양한 산업 분야의 추천시스템, 약물의 부작용 예측, 교통 체증 예측, 신약 개발 등 여러 분야에 적용될 수 있다.
3. Choice of Graph Representation
Graph의 구조에 대해 알아보자.

Graph(G(N,E))는 Nodes(N)과 Edges(E)로 구성된다.
Graph는 각 데이터(Nodes)간의 관계(Edges)를 잘 표현하는 common language라고 할 수 있다.

위 그림에서 네 예시 모두 같은 representation을 나타내고 있는데, 비슷한 ML 알고리즘으로 위 문제들을 동일하게 해결할 수 있을 것이다. 이처럼 적절한 Representation을 선택하는 것은 굉장히 중요하다.

적절한 Representation을 선택하기 위해선 각 nodes들 혹은 각 links(edges)들이 무엇인지를 정확하게 알고있어야한다.
Graph를 만드는 핵심은 바로 Nodes와 Edges가 무엇인지 정의하는 것 부터 시작한다고 할 수 있다.

Graph는 방향이 있는(Directed) 것과 방향이 없는(Undirected) 것으로 나눌 수 있다.

Undirected graph의 예시는 Facebook에서의 친구 관계 등이 있을 것이고,
Directed graph의 예시는 전화 수신/발신 목록 혹은 Twitter에서 팔로잉 여부 등이 있을 것이다.
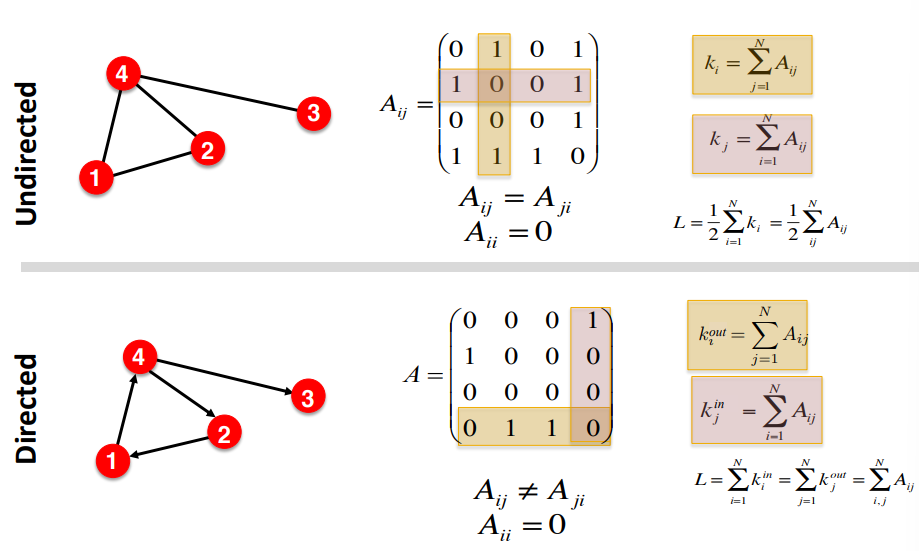
Node Degrees란 i번째 node에서 인접한 edges의 수를 나타낸다.
이는 Undirected일때와 Directed일때 구하는 방법이 조금 다른데, 아래와 같다.

Bipartite Graph는 nodes가 U와 V 집합으로 독립적으로 구분되어 각각의 집합 안에서는 연결되어있지 않은 graph를 의미한다. 예를들어 논문의 저자 - 해당 논문, 메뉴판의 음식 - 가격, 배우 - 영화, 사용자 - 영화 등의 예시가 있다.

이때, 이런 Bipartite의 정사영에 해당하는 Projection U 와 Projection V에 대해 생각해보면, 논문의 저자 - 해당 논문 예시에서 논문의 저자가 공동저자인 경우 U를 표현할때 이를 고려하여 나타낼 수 있을 것이다. 가령 아래의 예시에서 1번과 3번 저자가 A라는 논문을 공동으로 작성하였기 때문에, Projection U에서 1과 3은 edges로 연결되어있다. 반면, 3번과 5번 저자는 공동으로 작성한 논문이 없기 때문에 edges로 연결되어있지 않다. Projection V도 마찬가지인데, 논문의 입장에서도 A논문과 B논문 모두 2번 저자라는 공통의 저자가 있기 때문에 연결되어있고, 공통의 저자가 없는 논문들은 edges로 연결되어있지 않다.

그렇다면 이런 Graph 자료 구조를 어떤 식으로 표현할까?
인접 행렬과 연결 리스트 방식이 있다.
1. 인접 행렬 (Adjacency Matrix)
인접 행렬에서는 i번째 node와 j번째 node가 연결되어 있다면, 이를 Aij에 1로서 나타낸다.
즉 인접 행렬 A를 통해 i번째 행과 j번째 열을 통해 이에 해당하는 node가 연결되어 있는지를 확인하는 것이다.
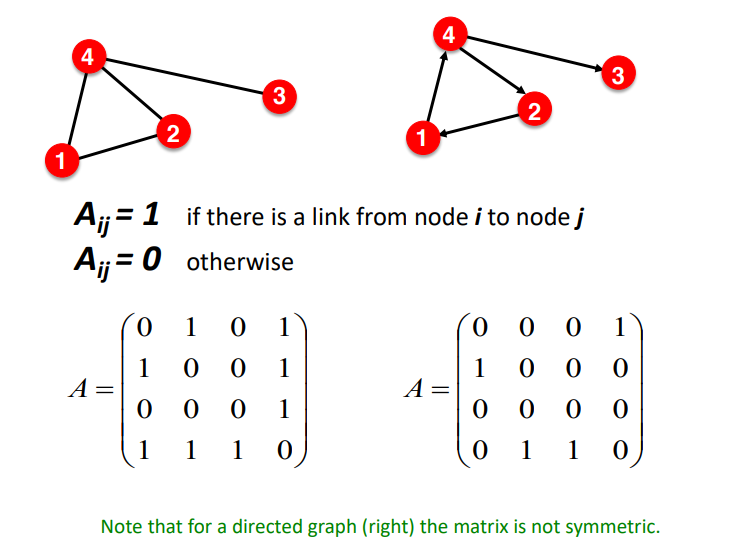
다만 현실에 있는 수많은 데이터들의 관계는 굉장히 sparse한 경우가 많다. 따라서 인접 행렬로서 이를 표현한다면 super sparse matrix를 얻을 가능성이 크다.


2. 인접 리스트 (Adjacency list)
이러한 문제점(sparse matrix)을 해결할 수 있는것이 바로 인접 리스트의 표기 방식이다.
인접 리스트는 각 리스트의 인덱스와 이에 연결되어있는 node를 리스트로서 나타낸다.

한가지 알아둬야 할 사항은 Graph의 각 Node와 Edge는 몇가지 속성을 가질 수 있는데, 이를테면 두 노드가 얼마나 관련이 있는지 그 정도를 나타내는 weight가 있을 수도 있고, 우선 순위에 해당하는 ranking이 있을수도 있다.
아래 사진은 node와 edge가 가질 수 있는 속성 목록이다.

다만, Graph가 weight 즉 가중치를 갖는 경우 인접 리스트보다는 인접 행렬로서 이를 나타내는 것이 더 쉬울 것이다.

위와 같이 인접 행렬의 각 행렬값에 1 혹은 0 이 아닌 가중치에 해당하는 값들을 표기함으로서 이를 나타낼 수 있다.
또 다른 예시로 node가 자기 자신과 연결되어 있는 self-edges graph나 두 node가 여러 edge로 연결되어 있는 Multigraph 등도 다음과 같이 인접 행렬로 표현할 수 있다.

마지막으로 Graphs의 connectivity에 대해 나오는데, directed graph의 경우 양 방향으로 edge가 있으면 이를 strongly connected directed graph라고 부른다.


4. Summary
1장에서는 Graphs는 어디에 쓰이고 왜 배워야 하는지, 또 어떤 task들이 있는지에 대해 알아보았다.
또 graph의 정의 및 다양한 종류, 표기 방법 등도 배울 수 있었는데, graph가 생각보다 훨씬 더 다양한 분야에 쓰이고 있는 것 같아 공부 시작하길 잘 했다는 생각이 든다.
'AI Theory > Graph Neural Network' 카테고리의 다른 글
| [CS224W 공부 노트] 2. Traditional Methods for ML on Graphs (1) (0) | 2022.10.27 |
|---|

댓글