목차
해당 포스팅의 모든 자료는 CS224W 강의 및 관련 자료를 바탕으로 정리하였습니다.
0. 들어가기에 앞서
1장에서는 graph의 정의(nodes,edges) 및 다양한 종류, 표기 방법 등도 배울 수 있었다.
또 이를 왜 배워야하고 어떤 task들이 있는지에 대해서도 알아보았다.
[CS224W 공부 노트] 1.Introduction; Machine Learning for Graphs
[CS224W 공부 노트] 1.Introduction; Machine Learning for Graphs
해당 포스팅의 모든 자료는 CS224W 강의 및 관련 자료를 바탕으로 정리하였습니다. 0. 들어가기에 앞서 경쟁력 있는 AI 개발자가 되기 위해서는, 다양한 딥러닝 학습 방법론을 바탕으로 주어진
hyunsooworld.tistory.com
이번 장에서는 graph의 feature들을 어떻게 design 할 것인지, 즉 전통적인 feature-based methods를 nodel level, link level, graph level에서 각각 알아보자.
(생각보다 분량이 길어 graph level은 다음 포스팅에서 작성하겠습니다.)
1.Traditional Feature-based Methods
1강에서는 graph를 활용한 task들의 종류로 Node-level prediction, Link-level prediction, Graph-level prediction이 있다는 것을 배웠다. 각각의 task들은 features로 node, link, graph를 갖는다.


전통적인 머신러닝 파이프라인은 다음과 같다.
1) 우선 데이터에 해당하는 nodes, links, entire graphs 등을 벡터(features)로서 표현한다.
2) 그 후에는 ML model을 활용하여 이를 학습시킨다. (model의 종류에는 Random forest, SVM, Neural network등이 있다.)

이번 포스팅에서는, 이러한 과정(feature design)에 대해서 알아보자.
모델의 좋은 성능을 위해서는 Feature Design을 잘 하는것이 핵심이다.
전통적인 머신러닝 파이프라인에서는 hand-designed, handcrafted features를 사용했다.

이러한 hand-designed features를 Node-level prediction, Link-level prediction, Graph-level prediction으로 케이스를 나눠서 생각해보자. (간결성을 위해 undirected graphs를 예시로 들겠다.)
수업의 목표는 design choices가 d 차원의 벡터인 피처를 갖는 objects의 set으로부터 좋은 예측을 하는 방법을 배우는 것이다.


2. Traditional Feature-based Methods: Node (node level)
가장 먼저 node level에서 살펴보자.
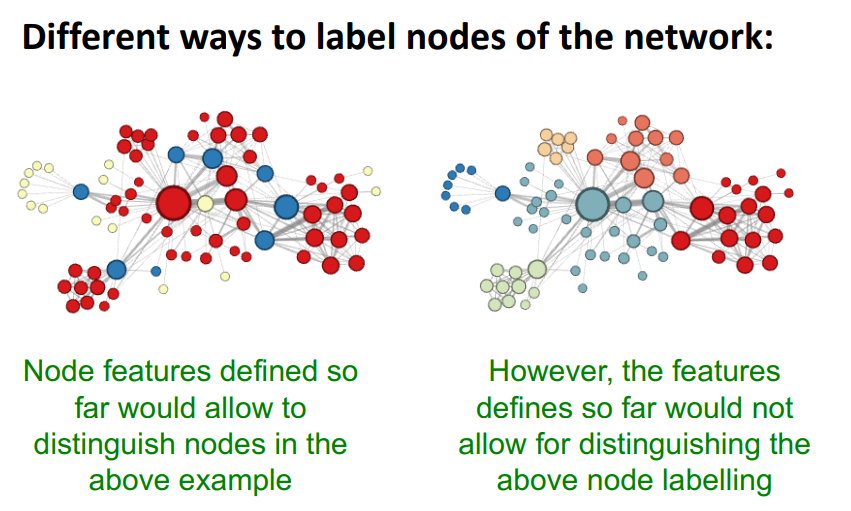
아래의 task는 초록, 빨간색 점이 몇 개 주어졌을때, 나머지 점들의 색을 예측하는 일종의 semi-supervised case다.


따라서 node level features의 목표는 위와 같은 network의 구조와 node의 위치를 잘 characterize하는 것이라고 할 수 있다.
이에 대한 접근법은 크게 네 가지로 나뉜다.
1) Node degree
2) Node centrality
3) Clustering coefficient
4) Graphlets
1) Node degree
Node degree 방법은 각각의 노드를 기준으로 인접하고 있는 노드 수인 degree를 구하는 것이다.
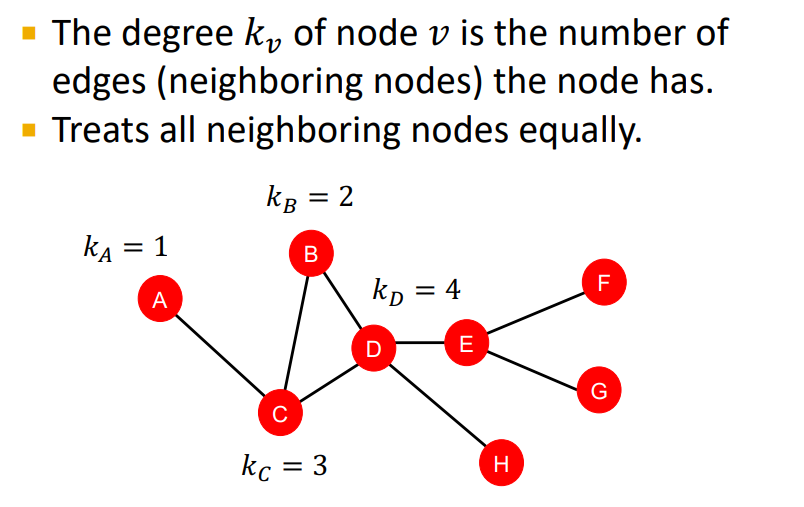
그러나 문제점은 degree만 가지고는 그 특성을 파악할 수 없다는 것인데, 가령 node C와 node E의 경우 둘 다 degree가 3 이기 때문에 이 정보만으로는 classifier가 이 둘을 분류할 수 없을 것이다.
2) Node centrality

Node centrality는 node의 중요도를 수치화해서 갖는다. node의 중요도를 구하는 방식은 여러가지가 있는데, 대표적으로 Eigenvector centrality, Betweenness centrality, Closeness centrality 등이 있다.
2-1) Eigenvector centrality


Eigenvector centrality는 기본적으로 "중요한 node v는 중요한 노드 u들에 둘러쌓여 있다" 라는 전제를 한다.
그래서 결국, 얼마나 많은 links로 연결되어 있냐 보다는 얼마나 중요한 노드들과 연결되어 있는지를 측정한다.
2-2) Betweenness centrality
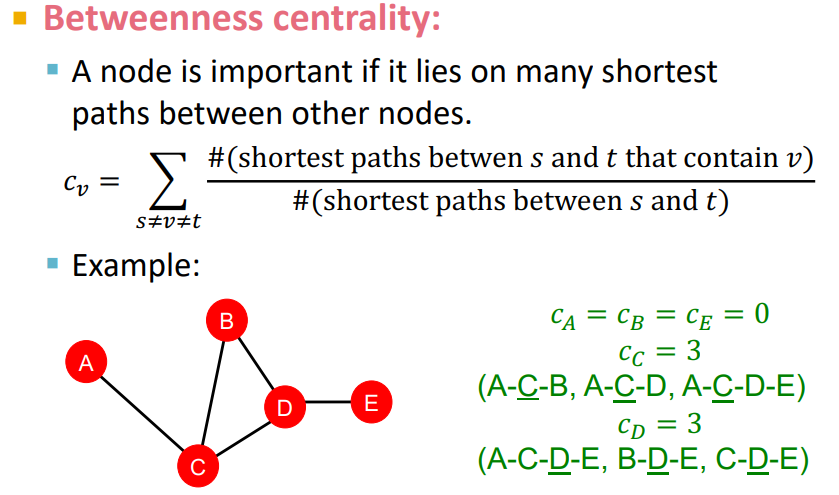
Betweenness centraility는 해당 노드가 서로 다른 두 노드 사이에 얼마나 많이 위치해 있는지를 측정한다.
이것의 핵심 아이디어는 중요한 connector(다리)에 해당하는 노드는 중요한 노드일 확률이 높다는 것이다.
2-3) Closeness centrality
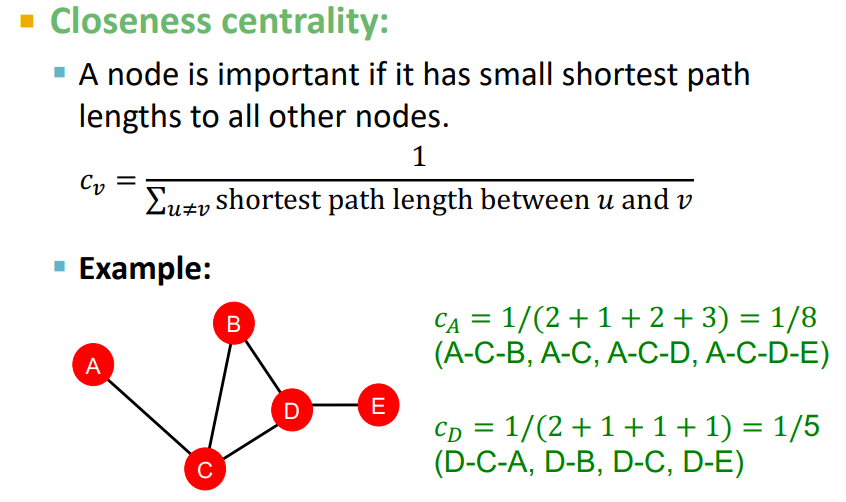
마지막으로 해당 node 기준으로 각각의 node들의 거리 합의 역수를 기준으로 적용하는 closeness centrality 방식이다.
3) Clustering coefficient
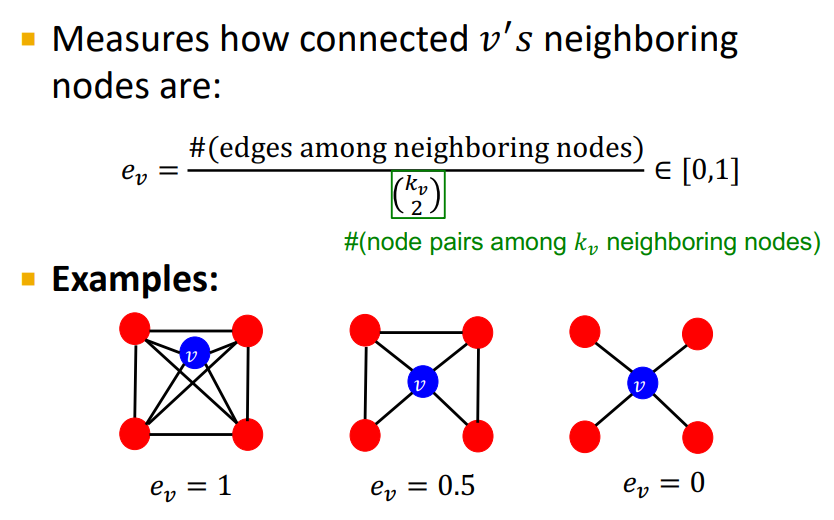
Clustering coefficient는 0에서 1 사이의 값을 나타낸다.
0인 경우 : 해당 노드와 인접한 노드들이 서로 각각은 인접하지 않는 경우
1인 경우 : 해당 노드와 인접한 노드들이 서로 모두 인접한 경우
4) Graphlets
아래와 같은 예시에서 자기 자신을 포함하고 있는 triangles의 수가 graphlets의 수다.
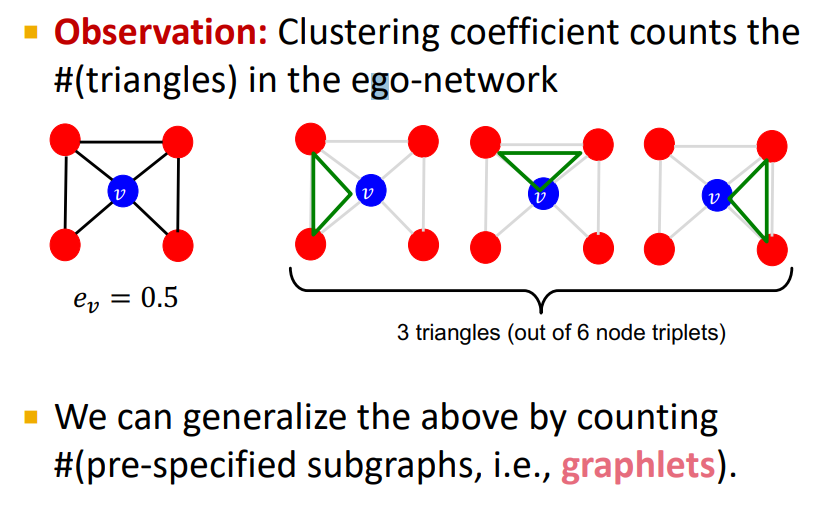
조금 더 일반화해보면, Graphlets은 rooted connected non-isomorphic subgraphs다.
이 말이 무슨말이냐면, root(기준 뿌리)로 부터 연결된 비동형 subgraphs라는 말이다.
isomorphic 즉 동형은 두 개 이상의 수학적 대상물이 표현 방법이 다를뿐, 구조상 같은 것을 의미한다.
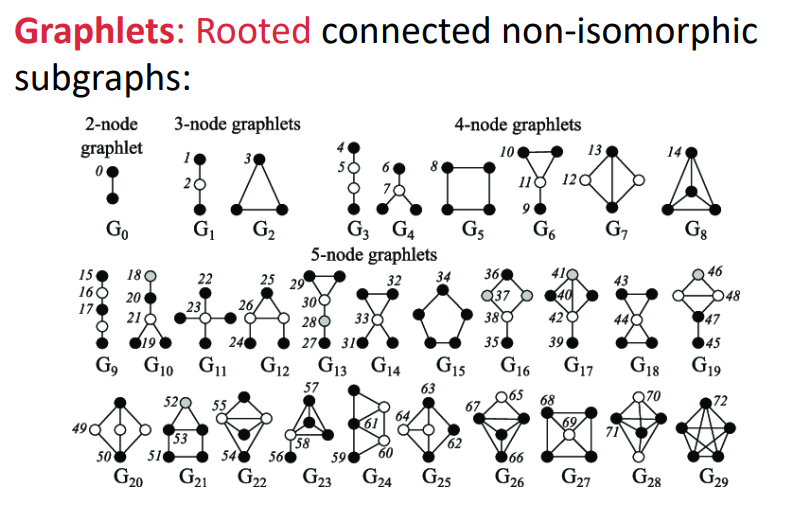
아래의 예시에서 하나의 그림(G0,G1,...G29) 별로 1개 이상의 기준 root 점이 표시되어있다.
이 점을 기준으로 생각해보았을때 나머지 점들은 다 이미 같은 구조로 여겨질 수 있기 때문에, 총 73개의 점 즉 graphlets의 수가 73개라고 할 수 있다. (2~5 nodes일때)
그렇다면 GDV는 무엇일까?
GDV(Graphlet Degree Vector)는 nodes들에 대한 graphlet 기반의 features다.

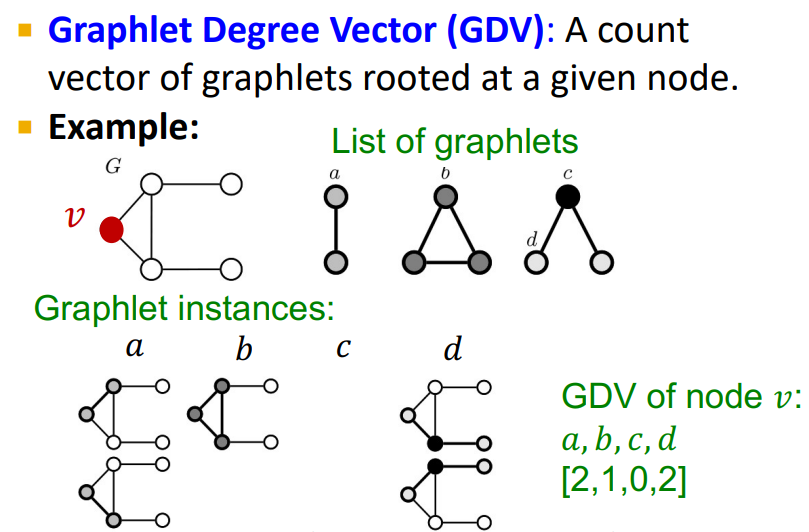
예를들어, 오른쪽 그림의 예시에서, 2 nodes의 graphlets을 기준으로 생각해 보았을때 총 graphlets의 종류는 3가지가 될 것이고, root가 될 수 있는 node는 a, b, c, d로 총 4개일 것이다. 각각에 대해 생각해보면 a는 2개의, b는 1개, c는 0개, d는 2개의 graphlets을 가질 것이고 이를 벡터로서 나타내면 [2,1,0,2] 가 될 것이다.

만약 2~5 nodes에 대한 graphlets을 고려한다면 총 73개의 root node가 나올것이다.

결론짓자면, node features는 두가지로 나뉠 수 있다.
Importance-based(중요도 기반)과 Sturcture-based(구조 기반)인데,
Importance-based에는 Node degree, Different node centrality measures가 있다.

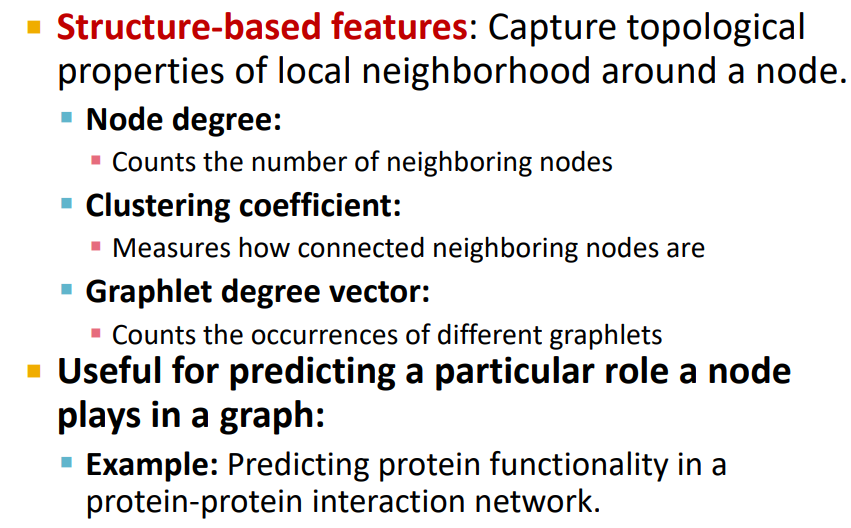
Structure-based에는 Node degree, Clustering coefficient, Graphlet count vector등이 있다.
3. Traditional Feature-based Methods: Link (link level)
Link level prediction task는 기존에 존재하던 link정보들을 토대로 새로운 link를 예측하는 것이다.
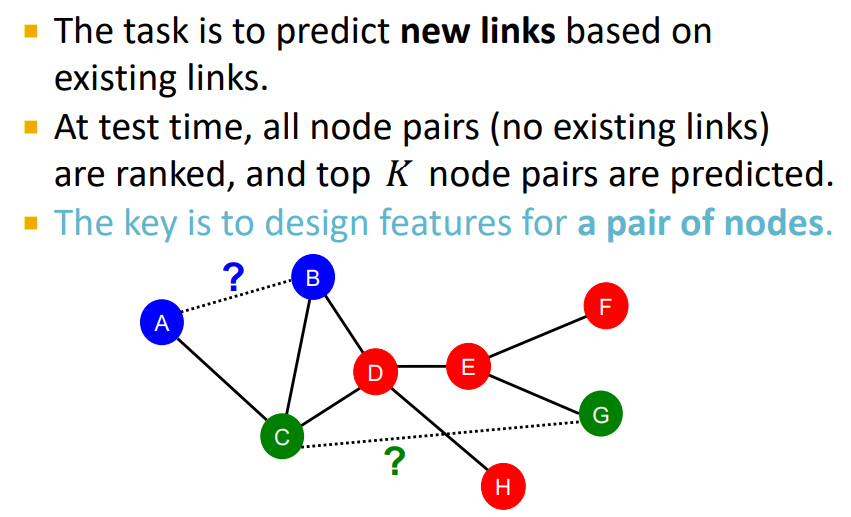
핵심은 a pair of nodes 즉 노드의 쌍에 대한 features를 잘 design해야한다는 것인데,
예를들어 해당 task(link level prediction)를 우리가 위에서 봤던 node level 방식으로 해결한다면(단순하게 각 node들의 feature concat) link들의 관계를 잘 나타낼 수 없을 것이다.

Link prediction task에는 두가지 형태가 있는데 1) Links missing at random과 2) Links over time이다
1) Links missing at random은 말 그대로 links 중 하나를 random하게 제거한 후 이를 다시 예측해내는 형태이다.
2) Links over time은 주어진 graph의 해당 time step 말고 그 이후 time step 상태를 예측하는 형태이다.
그렇다면 이러한 두 형태에서 pair of nodes가 주어졌을때 이에대한 feature 정보는 어떻게 제공할 것인가?
nodes 쌍 (x, y)에 대해서 일종의 score 점수인 c(x, y)를 구하고, 이를 정렬해서 top n개쌍을 새로운 links로서 예측할 수 있다.

두 노드의 관계를 나타내는 descriptor를 만들거나, 이를 featurize 하는 방법에는 크게 세 가지가 있다.
- Distance-based feature
- Local neighborhood overlap
- Global neighborhood overlap
가장 먼저 Distance-based feature 방법을 살펴보면 이는 말 그대로 거리 기반의 feature 정보로 나타내는 것이다.
아래 그림에서 B node와 H node를 예로 들면, 이 둘 사이의 거리는 2 이므로 S(B,H)는 2가 된다.
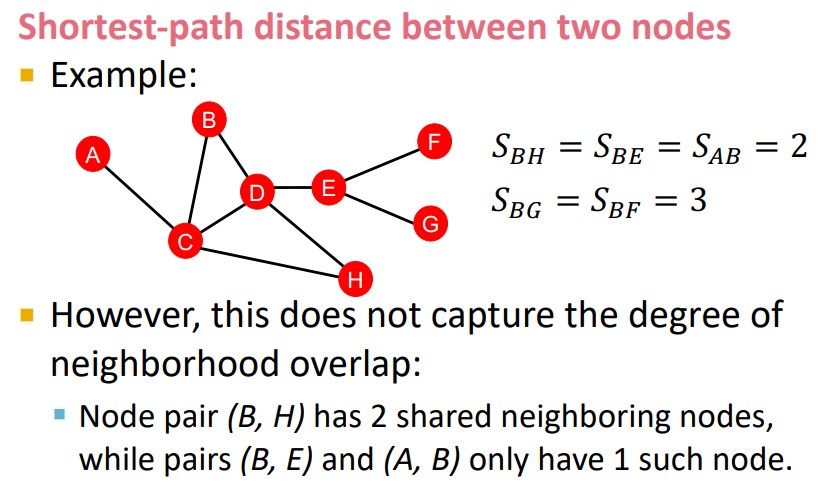
그러나 이러한 방식은 neighborhood degree에 대한 정보는 잡아내지 못하기 때문에 항상 좋은것은 아니다.
두번째는 Local neighborhood이다.
v1 node와 v2 node가 있다고 하면 단순히 겹치는 neighbors의 수를 사용하거나, Jaccard's coefficient(자카드 유사도) 혹은 Adamic-Adar index를 이용해 이를 나타낼 수 있다.
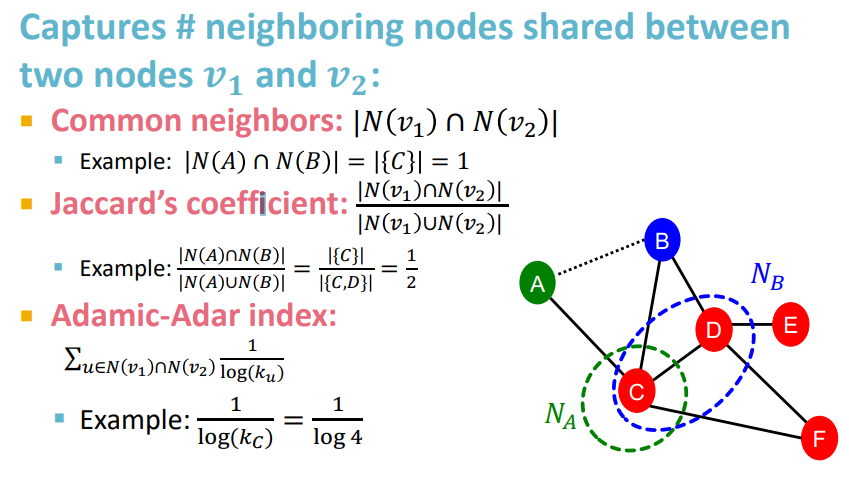
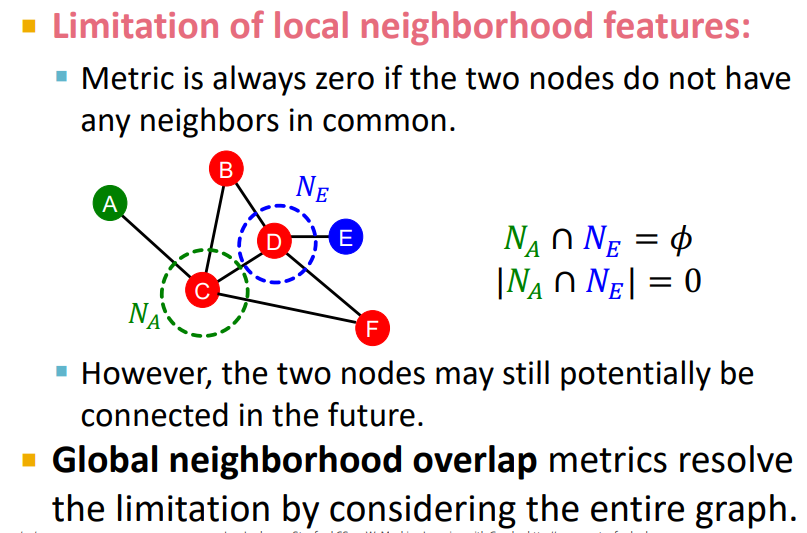
그러나 이러한 방식 역시 문제점이 있었는데, A node와 E node는 겹치는 neighbor이 없는데, 이러면 자카드 유사도를 따졌을때 항상 0이 나온다는 것이다.
그래서 제안된 것이 마지막으로 살펴 볼 Global neighborhood overlap이다.
우선 Katz index에 대해 알아보자.

Katz index란 주어진 두 노드 사이의 모든 길이의 경로 수를 계산하는 것이다.
이때 두 노드의 경로 수는 graph adjacency matrix를 이용해서 계산할 수 있다.
계산 방식은 아래와 같다.
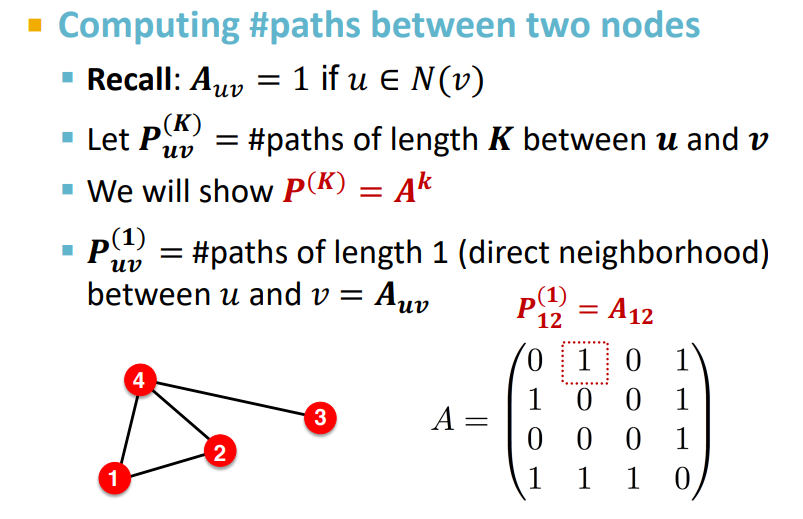

최종적으로 계산된 행렬을 보면 node 1 2 3 4 를 기준으로 다른 node와 연결되어있는 길이 2의 path 수를 표현하고 있다.
(이때 대각성분이 2,2,1,3인 이유는 동일한 경로로 왔다,갔다 할 수 있는게 각각 2,2,1,3개 있기 때문이다.)
다시 Katz index로 돌아와서, 이렇게 구한 Auv-l(index : l)를 가지고 아래 그림의 오른쪽 수식처럼 score에 해당하는 S(v1,v2)를 구할 수 있다.
💡A_l(v1, v2)는 v1 node와 v2 node 사이의 길이가 l 인 경로의 수를 의미한다.
A_l(v1, v2)앞에 붙은 β는 discount factor로서 길이 l 이 길어지는것에 가중치(weight)를 부여하는 역할을 한다.
이때 β > 1이면 긴 path에 더 큰 가중치를, β = 1이면 길이에 상관없이 모든 빈도를 더하고, 마지막으로 β < 1이면 짧은 path에 대해 더 큰 가충치를 부여한다.


정리하자면, 아래와 같다.
Traditional feature-based methods 중 link level의 경우 features를 표현하는 방법으로 Distance-based, Local neighborhood overlap, Global neighborhood overlap이 있다.
Distance-based feature는 이해하기 쉽고 직관적이지만, 두 노드간의 neighborhood 정보를 고려하지 못한다.
Local neighborhood overlap은 두 노드의 neighborhood 정보는 고려하지만 shared neighbor node가 없을 경우 (거리가 2 이상으로 떨어진 경우) 무조건 0 값이 나온다.
Global neighborhood overlap는 global graph structure를 사용하는데, 대표적으로 Katz index가 있다.

'AI Theory > Graph Neural Network' 카테고리의 다른 글
| [CS224W 공부 노트] 1.Introduction; Machine Learning for Graphs (0) | 2022.10.22 |
|---|

댓글